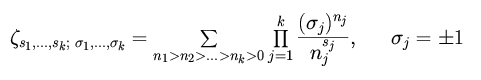
One of the problem of multiloop calculation of dimensional regulated Feynman diagrams is the extraction of analytical coefficients in epsilon-expansion. The important examples are massless propagator-type diagrams existing in the renormalization group calculations: the occurring transcendental numbers can be expressed in terms of multiple Euler-Zagier sums [1]:
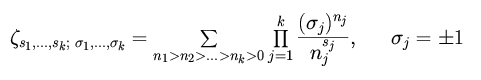
For lower cases, these sums correspond to ordinary zeta-functions.
In the 6-, 7-loop calculations of the beta-function in scalar theory [2]
the non-zeta, transcendental numbers,
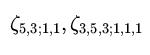 arises (Example of the 6-loop graph giving
non-zeta counterterm - picture from [3]).
Another example is the calculation of anomalous dimensions [3],
where another constant,
arises (Example of the 6-loop graph giving
non-zeta counterterm - picture from [3]).
Another example is the calculation of anomalous dimensions [3],
where another constant,
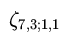 is appeared. A remarkable property of these constants, established by
Dirk Kreimer ,
is their connection with knots [4].
is appeared. A remarkable property of these constants, established by
Dirk Kreimer ,
is their connection with knots [4].
The transcendental structure of massive single-scale diagrams (when all parameters are equal to unity or zero), arising, for example, in multiloop massive calculations in QED or QCD within the on-shell scheme [5], is less investigated. To classify new constants appearing in this case, David Broadhurst has introduced the ``sixth root of unity'' basis [6] connected with
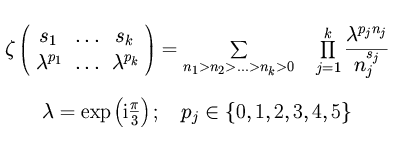
 of two possible angles,
of two possible angles,
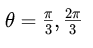 where
where
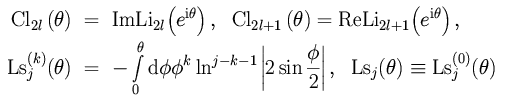 ,
,
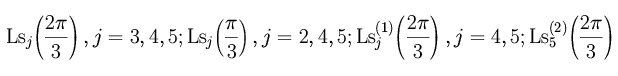
By analogy with the odd basis introduced in [7],
it is possible to consider the
even basis [9] connected with the angles
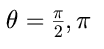 .
Apart from the well-known elements (see details in [1]), like zeta-function,
the Catalan's constant G,
.
Apart from the well-known elements (see details in [1]), like zeta-function,
the Catalan's constant G,
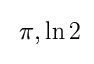 this basis also contains (up to the weight 5)
this basis also contains (up to the weight 5)
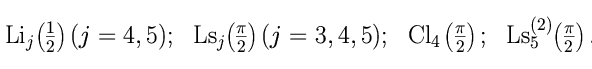
Later, in [10] a connection has been examined between our basis and binomial sums
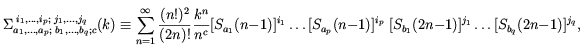
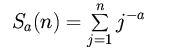 ,
is harmonic sum. In particular, these sums are connected with epsilon-expansion of
hypergeometric function of argument 1/4 (see Appendix B of Ref.[9]).
It was demonstrated [9], that one extra term
should be added to the odd weight-5 basis.
This new constant can be related to a special case of the multiple binomial sums.
For the even basis one needs to add
two additional constants of weight 5:
one is and second is
is the generalization of the log-sine integrals.
,
is harmonic sum. In particular, these sums are connected with epsilon-expansion of
hypergeometric function of argument 1/4 (see Appendix B of Ref.[9]).
It was demonstrated [9], that one extra term
should be added to the odd weight-5 basis.
This new constant can be related to a special case of the multiple binomial sums.
For the even basis one needs to add
two additional constants of weight 5:
one is and second is
is the generalization of the log-sine integrals.
For high precison numerical calculation of the proper constant the program LSJK has been developed [14].
[1]
D.J.Broadhurst,
hep-th/9604128
[2]
D.J.Broadhurst, D.Kreimer,
Int. J. Mod. Phys. C6 (1995) 519,
hep-ph/9504352
| [3] | D.J.Broadhurst, J.A.Gracey, D.Kreimer,
Z. Phys. C75 (1997) 559
hep-th/9607174 |
| D.J. Broadhurst, A.V. Kotikov,
Phys.Lett. B441 (1998) 345
hep-th/9612013 |
| [4] D.Kreimer, | Phys. Lett. B354 (1995) 117,
hep-th/9503059 |
| J. Knot Th. Ram. 6 (1997) 479,
q-alg/9607022 |
| [5] | N. Gray, D.J. Broadhurst, W. Grafe, K.Schilcher,
Z. Phys. C48 (1990) 673 |
| S. Laporta, E. Remiddi,
Phys. Lett. B379 (1996) 283
hep-ph/9602417 |
|
| K. Melnikov, T. van Ritbergen,
Phys. Lett. B482 (2000) 99
hep-ph/9912391 |
|
| Nucl. Phys. B591 (2000) 515
hep-ph/0005131 |
[6]
D.J.Broadhurst,
Eur. Phys. J. C8 (1999) 311,
hep-th/9803091
[7] J.Fleischer, M.Yu.Kalmykov, Phys. Lett. B470 (1999) 168, hep-ph/9910223
| [8] A.I.Davydychev, | hep-th/9908032 |
| Phys. Rev. D61 (2000) 087701,
hep-ph/9910224 |
[9] A.I.Davydychev, M.Yu.Kalmykov, Nucl. Phys. B605 (2001) 266, hep-th/0012189
[10] J.Fleischer, M.Yu.Kalmykov, A.V.Kotikov, Phys. Lett. B462 (1999) 169; 467 (1999) 310(E), hep-ph/9905249
[11] M.Yu.Kalmykov, O.Veretin, Phys. Lett. B483 (2000) 315, hep-th/0004010
[12] A.I.Davydychev, M.Yu.Kalmykov, hep-th/0203212
[13] M.Yu.Kalmykov, Nucl. Phys. B718 (2005) 276, hep-ph/0503070
[14] M.Yu.Kalmykov, A.Sheplyakov Comput.Phys.Commun. 172 (2005) 45, hep-ph/0411100