Inspiriert durch einen Vortrag von Herrn, Prof. Dr. T. Lohse der Humboldt Universität Berlin im Rahmen der Novembervorlesungen 2002 der HU-Berlin zum Thema „Das Rätsel der Teilchenstrahlung aus dem Weltall“ habe ich mich im Laufe des Jahres 2003 immer tiefer in die Materie eingearbeitet und interessante Erkenntnisse auch über nicht direkt involvierte Gebiete der Physik gewonnen, was letztlich den Entschluss dieses Thema für die Semesterarbeit zu wählen, bewirkte.

Bereits in dem Vortrag von Prof. Lohse wurde „H.E.S.S“ als Teleskopsystem zur Messung von kosmischen Gammastrahlen vorgestellt. Dieses stellt ein Gemeinschaftsprojekt von mehreren Forschungseinrichtungen und Universitäten dar, an dem unter anderem auch die Humboldt Universität zu Berlin mit beteiligt ist. Auch wenn dieses Projekt hier nur einen sehr kleinen Stellenwert einnimmt, war es doch ein interessanter Leitfaden, um den aktuellen Erkenntnisstand zu überschauen und zukünftige Experimente verstehen zu können. Das Observatorium ist mit der Aufnahme des Betriebes des vierten Teleskops am 10. Dezember 2003 nun voll einsatzbereit.

Das interessante am Thema kosmische Strahlung ist, dass viele Theorien zwar wohl durchdacht, jedoch – wenn überhaupt – auf sehr spärlichen Messdaten „aufgebaut“ sind, also noch auf ihre experimentelle Überprüfung warten. Daher ist diese Forschung absolut aktuell und auch allen „Schwankungen“ ausgesetzt. Dies lässt viel Raum für eigene Überlegungen, die im Rahmen einer Schülerarbeit jedoch wahrlich nicht zu erwarten sind. Diese Arbeit beschränkt sich darauf einen Überblick über die bestehenden Veröffentlichungen zum Thema zu geben.

An dieser Stelle möchte ich Herrn Prof. Dr. Lohse danken, der nicht nur durch seinen Vortrag das Interesse für das Thema geweckt hat, sondern auch ohne weiters bereit war Fragen meinerseits bei einem Besuch in Adlershof zu beantworten, sowie einen prüfenden Blick auf diese Arbeit zu werfen.

Nicht zulezt durch seine Ausführungen ist mir bewusst geworden, dass sogut wie alle hier präsentierten „Erkenntnisse“ auf dem Gebiet der kosmischen Strahlung nur als Theorien anzusehen sind und viele Vermutungen erst durch weitere Messungen bestätigt werden müssen. Alle hier vorgetragenen Ergebnisse und Vermutungen sind also nur als beste bis zum heutigen Tage bestehende Erklärungen anzusehen und keinesfalls zweifelsfrei belegt. Sollte dies an der einen oder anderen Stelle nicht deutlich genug zum Ausdruck kommen, so sei es jetzt für die gesamte Arbeit gesagt.

2. Historische Entwicklung

Gegen Ende des 19. Jahrhunderts benutzte man vorwiegend das Elektroskop um die Gegenwart von elektrischer Ladung zu demonstrieren.Um 1890 beobachteten Wissenschaftler, welche die Leitfähigkeit von Gasen mit Goldblattelektroskopen untersuchten, dass sich das Elektroskop stetig, wenn auch sehr langsam, entlud, egal wie gut sie die Versuchsanordnung abschirmten.1901 untersuchten J. Elster und H. Geitel in Deutschland sowie C.T.R. Wilson in England dieses Phänomen und kamen zu dem Schluss, dass es eine bisher unbekannte Quelle ionisierender Strahlung geben muss. Zu dieser Zeit schien die Erklärung des Phänomens offensichtlich – radioaktive Strahlung in der Atmosphäre und aus der Erde, welche die Luft um das Elektroskop ionisiert. Diese Erklärung wurde populär aufgrund der Entdeckung der Röntgestrahlung durch Conrad Röntgen sowie durch die Erkenntnis aus Bequerell's Entdeckung der Radioaktivität in einer Uraniumverbindung 1896, dass radioaktive Strahlung aus quasi jedem Material auf der Erde stammen kann.

Der holländische Physiker Th. Wulf entwickelte 1907 ein hochstabiles Elektroskop mit Ionisationskammer, welches er zum Testen dieser Hypothese auf den Eifelturm brachte. Würde die ionisierende Strahlung, welche das stetige Entladen eines Elektroskops verursacht, tatsächlich aus der Erde bzw. der erdnahen Umgebung stammen, müsste die Intensität mit zunehmender Höhe abnehmen. Laut Wulfs Messungen betrug die Intensität lediglich 64% des Erdniveaus, was dies zunächst zu bestätigen schien, doch war der Abfall weitaus schwächer als von ihm vorher berechnet.

Abbildung 2 Victor Hess

Der 28 jährige Österreicher Victor Hess verfolgte diese Versuche und beschloss der Sache selbst auf den Grund zu gehen. 1912 unternahm er mit einem eigens manipulierten Elektroskop nach Wulfs Bauart einen Ballonflug, auf dem er die Ionisierung in verschiedenen Höhen notierte. Erstaunlicherweise nahm sie zwar zunächst bis zu einer Höhe von 500m ab, stieg dann aber mit zunehmender Entfernung vom Erdboden stark an

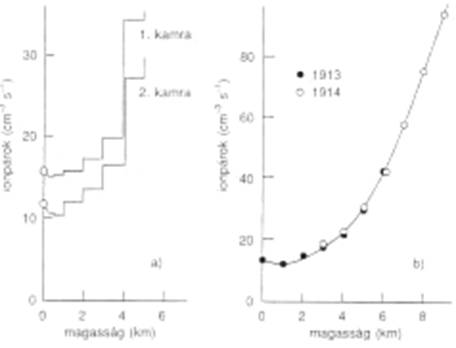
Abbildung 3 Messkurven der Ballonexperimente des Victor Hess (Intensität-Höhe)

Kolhörster[R 2] konnte später in 9km sogar die zehnfache Intensität feststellen. Hess sah für diesen Effekt keine andere Erklärung[R 1], als dass hochenergetische Strahung „von oben“ in die Atmosphäre eintritt und dort selbst in den eingschlossenen Ionisationskammern, die er mitführte, Ionisation herzuvorufen vermag. Diese Erkenntnis über die so genannte “Höhenstrahlung” lies ihn im Jahre 1936 an einem Nobelpereis teilhaben.

Aufgrund des ersten Weltkrieges kam die Erforschung der Höhenstrahlung in Europa zunächst zum Erliegen, doch der amerikanische Physiker R.A. Millikan begann sich für dieses Phänomen, dem er erstmals den Namen „kosmische Strahlung“ gab, zu interessieren und postulierte es handle sich hierbei um “Ultra-γ-Strahlung”, eine besonders energiereiche Form der γ-Strahlung(200MeV laut Berechnungen Milikans). Er hatte nicht nur selbst zusammen mit Bownen eigene Ballonmessungen unternommen, sondern auch in der Mitte von schneebedeckten Gebirgsseen keine deutliche verminderung der Ladungsabnahme eines aufgeladenen Elektroskops feststellen können. Letzteres wiegt besonders schwer, da Wasser und Schnee sowie Eis eines Gebirgssees so gut wie keine natürlich radioaktiven Stoffe beinhaltet.

Seine Theorie verschwand jedoch mit Bekanntwerden des Paarbildungsprozesses, welcher die Reichweite der γ -Strahlen sehr hoher Energien stark einschränkt. Der Niederländer J. Clay konnte 1927 zeigen, dass die Intensität der kosmischen Strahlung von der geometrischen Breite abhängt.Er fuhr mit seinen Ionisationskammern auf einem Segelschiff, welches zwischen den Breiten segelte. Er beobachtete eine Intensitätszunahme in höheren Breiten.

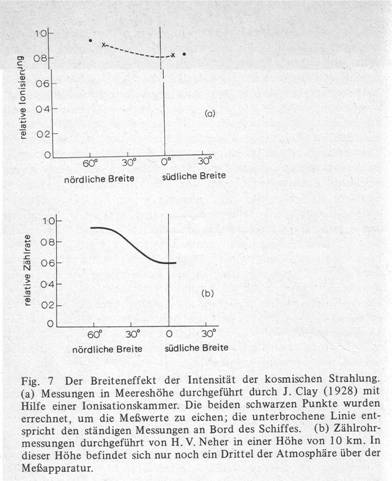
Abbildung 4 Der Breiteneffekt

Damit war klar, dass die „Höhenstrahlung“ zumindest teilweise aus geladenen Partikeln bestehen musste, da dieser Effekt nur mit einer Ablenkung dieser im Erdmagnetfeld zu erkären war. Dies bedeutete das Endgültige Aus für Milikans Photonentheorie, da diese keine elektrische Ladung aufweisen und somit keine Ablenkung erfahren können. Die primäre kosmische Strahlung kann an den Polen der Erde parallel zum Magnetfeld eindringen, während sie am Äquator senkrecht zum Erdmagnetfeld die volle Komponente der Lorentz-Kraft spürt. Daher können Teilchen einer bestimmten Energie nur bis zu einer von ihrer Energie abhängigen Breite auf der Erde nachgewiesen werden. Es ergeben sich also „verbotene“ Bereiche in der Erdmagnetosphäre, in der Teilchen einer bestimmten Energie niemals anzutreffen sein werden. Abbildung 5 verdeutlicht diese „verbotenen Bereiche“ für Teilchen ausgewählter Energien.

Abbildung 5 "Verbotene" und "erlaubte" Zonen für geladenen Teilchen

Kurioser Weise nahm die Intensität der Strahlung zwar vom Äquator an gemessen zu, von den mittleren Breiten (>35°) an war jedoch keine weitere Zunahme der Strahlung messbar.Dies liess sich dadurch erklären, dass die Teilchen der kosmischen Strahlung neben dem Magnetfeld der Erde auch die Atmosphäre überwinden müssen, in der sie durch Ionisierungen einen Energieverlust erleiden. Aufgrund dieses Energieverlustes können Teilchen niedrigerer Energie die Erdoberfläche nicht erreichen.

1930 bemerkte der italienische Physiker Bruno B. Rossi, dass, wenn die kosmischen Strahlen vorwiegend negativ oder vorwiegend positiv geladen sind, ein “Ost-West Effekt” zu beobachten sein müsste. Wären die kosmischen Partikel vorwiegend positv geladen, müsste die Mehrzahl von Westen kommen, bei negativer Ladung entsprechend von Osten.

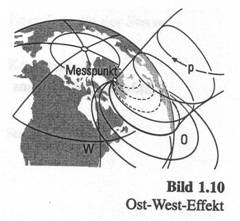
Abbildung 6 Der Ost-West-Effekt

Dies postulierte er basierend auf den von Störmer 1930 berechneten Bahnen geladener Teilchen im Erdmagnetfeld. Störmer, der ursprünglich das Phänomen der Polarlichter untersuchte, war bei Folgeexperimenten auch bewusst geworden, dass Teilchen bis zu einer bestimmten Energie auch vom Erdmagnetfeld eingefangen werden können.

2.1 Exkurs : Die Magnetosphäre und der Van-Allen Strahlungsgürtel

Das Magnetfeld der Erde wird durch das mittles dem Sonnewind ausgedehnten Magnetfeld der Sonne, der Heliosphäre, zu einer Kometenaritgen Form verformt. Elektrisch geladene Teilchen werden an der Magnetopause in unterschiedliche Richtungen abgelenkt, was zum Ost-West Effekt führt. Je geringer die Energie des Teilchens ist, desto stärker ist die Ablenkung. Daher können Teilchen niederer Energie nicht in niedere Breiten vorstoßen.

Abbildung 7 Die Magnetosphäre

Innerhalb der Magnetosphäre bilden sich verschiedene Strahlungsgürtel aus. In diesen Bereichen wirkt das Erdmagnetfeld als „magnetische Flasche“ und hält geladenen Teilchen gewisser Energien auf helixförmigen Bahnen gefangen. Diese Strahlungsgürtel wurden 1958 vom amerikanischen Forscher James Van Allen mittels des Satelliten Explorer 1 nachgewiesen und auch nach ihm benannt. Man unterscheidet zwischen zwei wesentlichen Bereichen : dem inneren und dem äußeren Strahlungsgürtel. Der innere Gürtel erstreckt sich in 1 bis 3 Erdradien Entfernung und besteht vorwiegend aus Protonen, welche aus zerfallenen Neuronen, die wiederum durch in der Atmosphäre wechselwirkende Partikel der kosmischen Strahlung entsanden sind, stammen. Die Protonengürtel sind über Zeiträume von bis zu 11 Jahren (einem Sonnenzyklus) stabil und nur geringen Variationen unterworfen.
Der äußere Strahlungsgürtel liegt weiter von Erdoberfläche entfernt und besteht im niederen Energiebereich (20-100 keV) aus Elektronen und Ionen. Dieses Phänomen wird auch als „Ringstrom“ bezeichnet. Im selben räumlichen Bereich finden sich jedoch auch Elektronen mit Energien im MeV Bereich, die unmöglich aus dem Sonnenwind stammen können. Dieser „outer radiation belt“(= äußerer Strahlungsgürtel) unterliegt sehr starken Schwankungen. Sowohl die räumliche Ausdehnung, als auch die Dichte und Intensität kann binnen von Minuten um das 1000 Fache schwanken. Die Quellen dieser Elektronen sind bis heute nicht vollständig geklärt. Man nimmt an, dass sie innerhalb der Magnetsphäre, genauer im Magnetotail beschleunigt werden. Dabei wird die Energie der solaren Schockwellen in einem Prozess genutzt, der noch nicht vollständig verstanden ist.

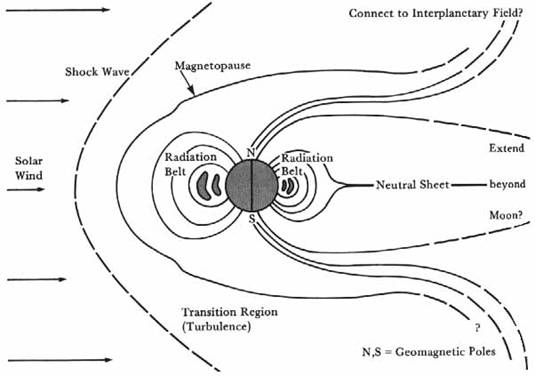
Abbildung 8 Die Magnetosphäre

Im Jahre 1929 entwickelten Bothe und Kolhöster eine spezielle Methode um die Entladung von zwei oder mehreren getrennten Geiger-Müller-Zählrohren anzeigen zulassen. Diese neue Methode der “Koinzidenzzählung” ermöglichte es die Bahn eines geladenen Teilchens durch die Zählrohre hindurch zu verfolgen. Eine Anordnung von Zählern, die so aufgestellt sind, dass sie nur eine Entladung anzeigen, wenn sie geradlinig von einem Teilchen durchlaufen werden nennt man Zählrohrteleskope. Mit diesen war es nun auch möglich die Richtung, aus denen die geladenen Teilchen kommen, festzustellen. Tatsächlich fallen die Teilchen bevorzugt senkrecht auf die Erde ein, hingegen sinkt die Einfallsintensität allmählig auf Null, wenn man die Apparatur gegen den Horizont neigt. Dies scheint auch logisch, da die nicht senkrecht einfallenden Teilchen ja eine viel dickere Luftschicht durchdringen müssen. Mit der Dicke der Luftschicht fällt die Häufigkeit der Teilchen natürlich rasch ab – da nur noch besonders energiereiche Teilchen “durchkommen”.

Mit Hilfe dieses Intsrumentes gelang es dem amerikanischen Physiker Thomas H. Johnson 1935 zu zeigen, dass die Ionisierungsrate vom östlichen zum westlichen Bobachtungswinkel hin anstieg, was belegte das die kosmischen Partikel eine überwiegend positive Ladung tragen. Er hatte somit den von Rossi theoretisch vermuteten Ost-West-Effekt beobachtet. Heute weis man zwar, dass der überwiegende Teil der kosmischen Strahlung Protonen sind, die positiv geladenen Teilchen auf Erdniveau jedoch positiv geladene Myonen () darstellen.

Die Koinzidenzzähler vermochten aber noch weit mehr über die kosmische Strahlung zu verraten. So hatte man teilweise Geigerzähler, die so aufgestellt waren, dass sie niemals durch ein einzelnes geradlinig einfallendes Teilchen gleichzeitig hätten entladen werden können, beobachtet, die dennoch eine Koinzidenzentladung registrierten. Als logische Schlussfolgerung musste man annehmen, dass die Teilchen nicht einzeln auftreten, sondern in manchen Fällen offensichtlich in sehr viel größeren Mengen. Erste Beobachtungen dieser “kosmischen Strahlenschauer” hatte D. Skobelzyn zufällig bei Experimenten in Leningrad unternommen. Beim Fotografieren der Nebelkammerspuren von β-Teilchen in einem starken Magnetfeld (0,15 T) waren ihm auf manchen seiner Aufnahmen Spuren von senkrecht einfallenenden Teilchen aufgefallen.

Abbildung 9 Pierre Auger

1938 führte der französische Physiker Pierre Auger dann Messungen mit beweglichen Zählrohrteleskopen in den Alpen durch, die endgültig die ganze Bedeutung dieser “Schauer” offenbarten. Er hatte bobachtet, dass die beiden Detektoren auch bei Distanzen von bis zu 75m noch die Ankunft von Partikeln zu exakt derselben Zeit registrierten. Auger hatte damit die Existenz der ausgedehnten Luftschauer (extensive air showers – EAS), deren Ausdehnung sich später als noch weit größer herausstellen sollten, belegt.

Rossi hatte bereits 1933 wichtige Erkenntisse darüber gewonnen. Er hatte Bleiplatten verschiedener Stärken vor Koinzidenzzählrohren, die nicht auf einer Geraden lagen, montiert. Er fand heraus, dass einfallende Teilchen nicht einfach absorbiert wurden, sondern bei Dicken von 1-2 cm eine größere Zählrate als ohne Bleiabschirmung hervorriefen. Offensichtlich wurden die Schauer nicht absorbiert sondern eher verstärkt dadurch dass sich der Schauer in der Bleischicht schnell weiterentwickelt und so hinter der Bleischicht viel mehr Teilchen austreten können als ursprünglich eingetreten waren.

Abstrahiert stellte man fest, dass die kosmische Strahlung ihren Ursprung zwar in den Tiefen des Weltalls hat, aber zumindest einige der registrierten Teilchen irdischen Ursprungs sind. Neben der aus dem Kosmos stammenden primären kosmischen Strahlung existiert also auch eine Sekundärstrahlung, die aus Wechselwirkung der primären Partikel in der Atmosphäre und in anderen Materialien entsteht.

Abbildung 10 Die Spur eines der ersten beobachteten Positronen

Bis zu ungefähr diesem Zeitpunkt waren als Elementarteilchen lediglich das Elektron, das Proton sowie das Photon bekannt. Als der amerikansiche Physiker Carl D. Anderson im Jahre 1932 die Krümmung der Linien, die kosmische Strahlen in einer Nebelkammer mit einem starken Magnetfeld hinterlassen, untersuchte, musste er feststellen, das die kosmischen Partikel viel zu schnell durch die Kammer flogen, um irgeneine Krümmung feststellen zu können. Um sie abzubremsen benutzte er eine Bleischicht. An eben dieser beobachtete er sodann eine Spur, die exakt zu einem Elektron gepasst hätte, wäre sie nicht in die falsche Richtung gebeugt. Damit hatte Anderson das Postitron, das 1928 von Dirac vermutete Antiteilchen des Elektrons, entdeckt und somit zusammen mit Chadwick, der 1932 das Neutron entdeckte, ein neues Zeitalter der Elementarteilchenphysik eingeläutet, aus der später die Astroteilchenphysik erwachsen sollte.

2.2 Die kosmische Hintergrundstahlung :

Abbildung 11 Penzias und Wilson vor der Bell Radioantene

Im Jahre 1965 arbeiteten Arno A. Penzias und Robert W. Wilson an einer extrem sensitiven Radioantenne in den Bell Telephone Laboratories in Murray Hill, New Jersey. Dabei hatten sie mit permanenten Störgeräuschen zu kämpfen. Bei der Suche nach Störungsquellen fanden sie unter anderem Tauben, die in der Antenne genistet hatten, beim Überprüfen der Anlage. Doch auch nach der Umquartierung der ungebetenen Gäste war ein dauerhaftes Störgeräusch vorhanden. Sie richteten die Antenne direkt auf New York City und dann in eine eher unbewohnte Richtung ohne einen Unterschied feststellen zu können. Die Störsignale waren also nicht zivilisationsbedingt, kamen daher auch nicht von irdischen Quellen.

Zeitgleich suchten Wissenschaftler der Princeton University unter der Leitung von Robert Dicke nach der durch die Urknalltheorie vorhergesagten kosmische Hintergrundstrahlung. Dieses Relikt des frühen Universums müsste heute im Mikrowellenbereich liegen und zeugt von einem Zustand nur wenige 100 000 Jahre nach dem Urknall. Als sie von den Daten aus den Bell-Laboratorien hörten war ihnen sofort klar was dort entdeckt worden war. Somit lieferten die Bell Forscher mehr oder weniger zufällig den bislang tatkräftigsten Beweis für die Urknalltheorie eines expandierenden Universums, welche bereits 1948 von George Gamov aufgestellt wurde.[R 3] Dafür teilten sich Penzias und Wilson 1978 den Physik-Nobelpreis.

Nach Gamov stellte das frühe Universum eine extrem heißes und dichtes „Plasma“ im thermischen Gleichgewicht dar und emmitierte daher thermische Stralung. Als diese Masse etwa 300.000 Jahre nach dem Urknall auf einige tausend Grad Kelvin abgekühlt war, bildeten sich einfache Wasserstoffatome und es setzte somit die „Rekombination“ ein. Die Photonen, welche zuvor stehts in Wechselwirkung mit den freien Elektronen getreten waren, bewegten sich fortan nahezu ungestört, da sie nicht mehr mit den Elektronen in Wechselwirkung treten konnten.

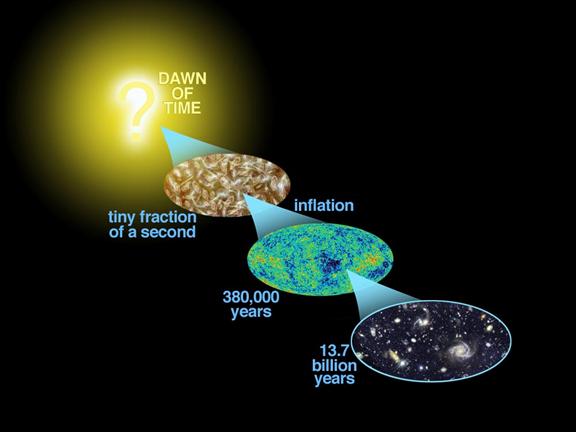
Abbildung 12 Die Entwicklung des Universums

Das Universum war nun transparent, sodass die Photonen sich frei und ungestört bewegten konnten. Aufgrund des expandierenden Universums und dem Dopplereffekt ist diese Strahlung heute soweit verschoben, dass ihr Maximum im Mikrowellenbereich liegt.

Abbildung 13 Das Intensitätspektrum der kosmischen Hintergrundstrahlung in Abhängigkeit von der Wellenlänge der Photonen gemessen durch den Cosmic Background Explorer (COBE)

Die kosmische Hintergrundstrahlung stellt ein nahezu perfektes Schwarzkörperspektrum bei einer Temperatur von 2.735 Kelvin dar. Dies wurde 1992 mit dem Cosmic Background Explorer (COBE) der Nasa nachgewiesen. Sie scheint desweitern isotrop über den Himmel verteilt. Doch gelang es durch genaue Messungen mit COBE Anisotropien nachzuweisen Diese Abweichungen, die bei liegen, wurden kürzlich durch die „Wilkinson Microwave Anisotropy Probe“(WMAP) der NASA genauer untersucht. Diese leichten Fluktuationen sind auf Fluktuationen der Dichte des frühen Universums zurückzuführen. Fluktuationen, aus denen möglicherweise später Galaxien entstanden. Sie zu untersuchen wird vermutlich einen entscheidenden Teil der Geschichte unseres Universums und der Urknall-Theorie eröffnen. Die Photonen der kosmischen Hintergrundstrahlung ermöglichen uns den weitesten Blick zurück zu den Anfängen des Universums : nahezu 13 Milliarden Jahre.

Abbildung 14 Die kosmische Hintergrundstrahlung gemessen durch COBE und WMAP

Die grundlegende Entwicklung unseres Universums ist trivial betrachtet ein kontinuierlicher Kampf zwischen der Gravitation und der Expansion. Da die Stärke der Gravitation ultimativ durch die durchschnittiche Dichte der Materie bestimmt ist, ergibt sich, dass die Entwicklung unseres Universums bereits vorrausbestimmt ist. Sollte eine gewisse „kritische Dichte“ überschritten werden, so wird das Universum eines Tages aufhören zu expandieren und wieder in sich zusammenstürzen. Ist dies nicht der Fall handelt es sich um ein „offenes“ Universum, welches für immer expandiert. Mithilfe der WMAP konnte nun nochmals bestätgt werden, dass die grundlegenden Parameter unseres Universums auf ein offenes Universum ( ) hindeuten und wir aller Wahrscheinlichkeit nach in einem in der Raumzeit „flachen“ Universum leben. Durch genaue Untersuchungen der winkelabhängigen Intensitätsschwankungen der Hintergrundstrahlung konnten desweiteren fundamentale Größen des Universums wie die Hubble Konstante mit erhöhter Genauigkeit bestimmt werden. (Anm. V. Prof. Lohse : Die große Überraschung ist, dass der Großteil (70%) von Ω durch eine unbekannte „dunkle Energie“ zu erklären ist (Vgl. Kosmologische Konstante). Diese wirkt wie eine Art Antigravitation und treibt unser Universum sogar beschleunigt auseinander.)

Abbildung 15 Die 3 möglichen Formen des Universums : geschlossenes, offenes oder flaches Universum

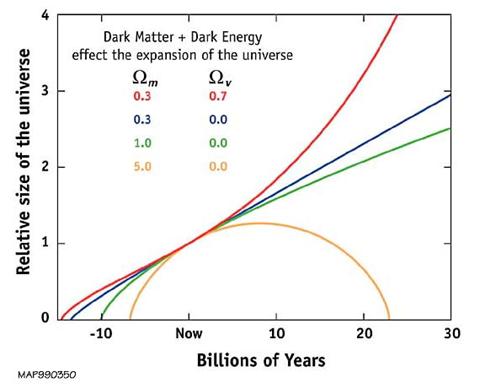
Abbildung 16 Relative Größe des jeweiligen Universums in Abhängigkeit von seinem alter. Ωm symbolisiert hierbei das Verhältnis von Dichte des Universums und kritischer Dichte. Entspricht die Dichte des Universums genau der Kritischen Dichte, so ist Ω=1.

3. kosmische Strahlung

3.1 Das Spektrum und seine Besonderheiten

Die in den Quellen beschleunigte kosmische Strahlung wird üblicherweise als „primäre kosmische Strahlung“ bezeichnet, wärend man die aus dieser Primärstrahlung durch Wechselwirkung hervorgegangenen Teilchen als sekundäre kosmische Strahlung bezeichnet. Was die geladene Komponente angeht, so besteht die kosmische Strahlung bei Energien als solche zu 98% aus Atomkernen und zu 2 % aus Elektronen. 87 % der Kerne sind Protonen, 12 % Heliumkerne(α-Teilchen) und nur 1 % schwerere Kerne. Diese Verteilung scheint zu den Grenzen des Spektrums, also bei sehr kleinen und sehr großen Energien verschoben zu sein. Die ungeladene Komponente stellen vordergründig Photonen und Neutrinos. Bisher wurden keine nennenswerten Hinweise auf Antimaterie in der kosmischen Strahlung entdeckt, was auch die Präsenz von Antimaterie im Kosmos als zunhemend unwahrscheinlich oder zummindestens unbedeutend erscheinen lässt. Zwar wurden durch Ballonexperimente einzelen Antiprotonen gemessen, diese stammen mit an Sicherheit grenzender Wahrscheinlichkeit aus sekundären Wechselwirkungen.

Betrachtet man die Elementhäufigkeit der primären kosmischen Strahlung im Vergleich zur Elementhäufigkeit in unserem Sonnensystem, so bemerkt man bei den Elementen Lithium, Beryllium und Bor, sowie bei den Elementen “unterhalb” von Eisen (Z < 26) eine größere Häufigkeit. Diese kann nur durch Fragmentation bzw “Spallation” der schwereren Kerne O, C und N bei der Kollision mit Materie im interstellaren Raum erklärt werden. Ebenso führt der „Zerfall“(nur bei Kollisionen) des relativ häufigen Elementes Eisen zu einer Häufung der unterhalb von Eisen liegenden Elemente. Die allgemein mit höherer Ordnungszahl abnehmende Häufigkeit lässt sich mithilfe der Kernphysik erklären, wonach kleinere Kerne stabiler sind und bestimmte Proton/Neutron-Konfigurationen energetisch bevorzugt zu sein scheinen. Kerne mit gerader Protonen- und Neutronenzahl erweisen sich hierbei als besonders stabil, während Kerne mit ungeraden Nukleonenzahlen am wenigsten stabil sind.

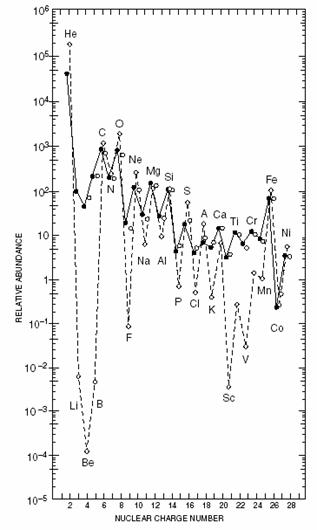
Abbildung 17 Häufigkeiten der Elemente in der kosmischen Strahlung im Vergleich zur Elementhäufigkeit im Sonnensystem (gestrichelt)

Sehr viel interessanter als die Elementhäufigkeit ist jedoch das Energiespektrum der kosmischen Strahlung. Die Gesamtenergie der auf die Erde einfallenden Teilchen ist vergleichbar mit der Energie des gesamten Sternenlichtes welches uns erreicht. Dabei können einzelne Teilchen jedoch beinahe unvorstellbar große Energiemengen tragen. Die energiereichsten Teilchen, die man bisher beobachtet hat, besaßen eine Energie der Größenordnung von bis eV. (In einer Oktobernacht 1991 wurde durch den “Fly's Eye”-Detektor in Utha, USA ein Teilchen mit gemessen – das entspricht etwa einer Energie von 50 Joule! ) Die Maximalenergie des Spektrums ist noch völlig offen, vom GZK-Cutoff, welcher weiter unten erkärt ist, einmal abgesehen. Der Fluss (dieser entspricht den Partikeln pro Fläche, pro Zeiteinheit, pro Winkel) der primären kosmischen Strahlung lässt sich in Teilen durch ein Potenzgesetz beschreiben.

Es gilt : , wobei N die Anzahl der eintreffenden Teilchen und E deren Energie ist.

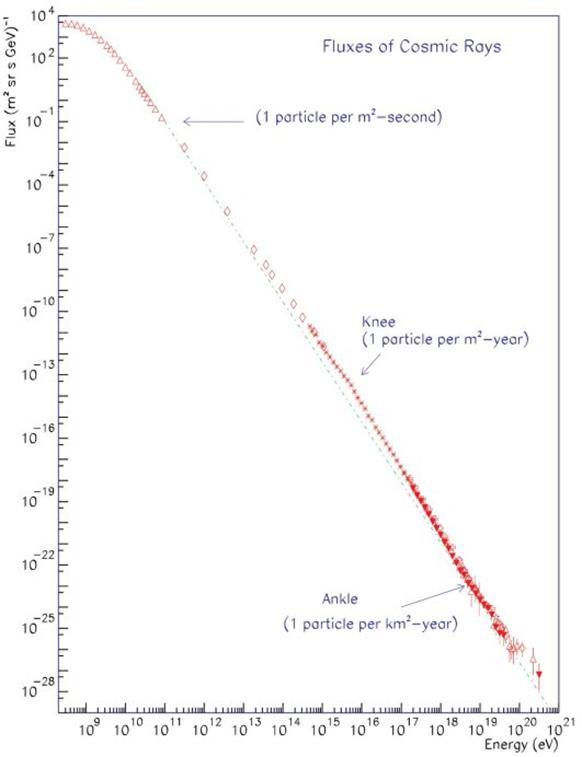
Abbildung 18 Das Energiespektrum der kosmischen Strahlung auf der Erde (Fluss der Strahlung in Abhängigkeit von der Energie des Teilchens)

Der erste Bereich erstreckt sich von den niedrigsten Energien bis hin zum sogenannten „Knie“ des Spektrums (E= eV). Hier gilt γ2,7. Als Quellen für Partikel dieser Energien kommen vor allem Supernovaexplosionen in Frage. Da diese in etwa alle 30 Jahre in unserer Galaxie auftreten, wäre die “ausreichende Versorgung” mit diesen Teilchen hierdurch hinreichend geklärt. Die kosmische Teilchenstrahlung ist zum überwiegenden Teil galaktischen Ursprungs. Das Magnetfeld unserer Galaxis kann jedoch nur Teilchen „festhalten“, deren Energie eV ist, da ansonsten die Gyroradien größer sind, als der Radius der Milchstraße selbst. Man erhält für den Gyroradius durch Gleichsetzten von Radial- und Lorentzkraft, bei und :

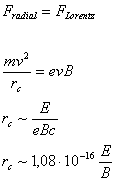
Das Knie selbst lässt sich sowohl dahingehend interpretieren, dass beieV die Teilchen beginnen die Milchstraße zu verlassen, als auch dass Supernovaexplosionen Teilchen nur auf diese Energien beschleunigen können und somit für Teilchen höherer Energie ein anderer Beschleunigungsmechanismus verantwortlich sein muss. An das Knie des Spektrums schließt sich ein etwas steiler fallender Bereich bis zum “Knöchel” bei E= eV an. Hier gilt : γ 3. Die Quellen hierfür sind aller Wahrscheinlichkeit nach aktive galaktische Kerne und Akkretionsscheiben um „kleinere“ schwarze Löcher. Danach flacht das Spektrum wieder zu γ 2,7 ab. Partikel dieser Energie müssen extragalaktischen Ursprungs sein, so wird im allgemeinen angenommen. Potentielle Quellen hierfür wären Akkretionsscheiben um supermassive schwarze Löcher im Zentrum von Galaxien, sogenannten aktive galaktische Kerne (AGN).

Interessanter Weise müsste es jedoch bei E eV der sogenannte „Greisen-Zatsepin-Kuzmin Cut-off“ [R 4] eintreten, da Protonen mit diesen Energien mit den 2,7K-Photonen der kosmischen Hintergrundstrahlung wechselwirken und Pionen erzeugen, was zu einem Energieverlust führt.

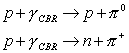
Die Schwellenwertenergie lässt sich mit den heutigen Messwerten über die kosmische Hintergrundstrahlung berechnen durch :

, bei T=2,728K .

Dies müsste die absolute Obergrenze im Spektrum darstellen Doch auch schon bei Energien von eV ist die mittlere freie Weglänge der Protonen so gering, dass sie nur noch von Quellen innerhalb unserer Milchstraße zu uns gelangen können.

Dieser theoretisch vermutete Cutoff bereitet einige Schwierigkeiten, da die Daten hierzu widersprüchlich sind und er in der Praxis nicht zu existieren scheint. Das einige Luftschauerteleskope „Ereignesse“ mit Energien bis eV regestrierten gibt also neue Rätsel auf. Bei einer

Bei einer mittleren Dichte der Photonen der kosmischen Hintergrundstrahlung von : ergibt sich eine freie Weglänge, also eine mittlere Weglänge ohne Kollision, von 6 MPc. Bei einem Energieverlust von rund 20 % pro Stoßvorgang ergibt sich eine maximale Distanz von rund 160 MPc bei Protonen von eV. Innerhalb dieser Distanz sind aber bislang keine Objekte bekannt, die Teilchen auf solch hohe Energien beschleunigen können. Die höchste bisher beobachtete Teilchenenergie betrug 3,2 und wurde, wie bereits erwähnt, im Oktober 1991 vom Fly’s Eye Teleskop gemessen.

3.2 Exkurs : Erklärungsmodelle für hochenergetische Teilchen (Extreme High Energy CR)

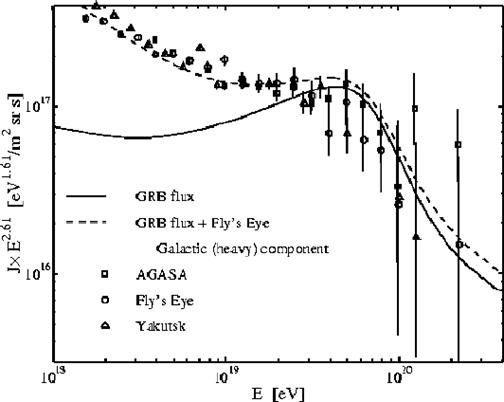
Abbildung 19 Der Fluss der hochenergestischen kosmischen Strahlung

Die Herkunft der beobachteten kosmischen Strahlung mit extrem hoher Energie (EHE) also die mit Energien ist eines der wesentlichen, ungelösten Probleme der modernen Astrophysik. Es wurden bisher in etwa 20 dieser Ereignisse in der Literatur veröffentlicht, das höchste wie oben bereits erwähnt vom Fly’s Eye Teleskop. Da die Energie der EHE-kosmischen Strahlung nur indirekt über ausgedehnte Luftschauer (EAS) gemessen werden kann, ist die Natur dieser EHE Teilchen größtenteils unbekannt. Außerdem sind Ereignisse dieser Größenordnung extrem selten, was die Erforschung erschwert. (1 Teilchen / km² / Jahrhundert bei eV) Aller Wahrscheinlichkeit nach handelt es sich um Kerne, aber auch Photonen können zu diesem Zeitpunkt noch nicht ausgeschlossen werden
Die Erklärung des Auftretens solcher EHE-Ereignisse ist mit zwei wesentlichen Problemen behaftet. Zum einen ist es extrem schwierig Teilchen auf diese Energien zu beschleunigen, zum anderen gibt es nicht genügend Quellen-Kandidaten in der „näheren Umgebung“ (100 Mpc) die für den Vorgang in Betracht kämen. Weiter entfernte Quellen sind wegen des GZK-Cutoff quasi ausgeschlossen. Auch Photonen unterliegen einer Entfernungsbegrenzung aufgrund des Paarbildungsprozesses, welcher viel früher einsetzt, weshalb Photonen eigentlich ausgeschlossen werden können.
Aufgrund dieser Erklärungsschwierigkeiten innerhalb der konventionellen Physik kommen Theorien über eine „neue Physik“ außehalb des Standardmodells der Elementarteilchen auf. Diese Vorschläge fallen meistens in zwei Klassen : In der einen wird versucht der GZK-Cutoff Entfernung auszuweichen oder den GZK-Cutoff Effekt im Energiespektrum zu umgehen indem man eine „neue Physik“ einführt. In der anderen nimmt man schlicht an, dass EHE Partikel beim Zerfall von supermassiven Teilchen (Masse > eV), welche aus fundamentalen Prozessen des frühen Universums stammen („Relikte“), entstehen. Diese nennt man zumeist “top-down Szenario“ im Gegensatz zum „bottom-up Szzenario“ bei dem das Teilchen von niedrigen Energien zu hohen Energien beschleunigt wird.
Beispiele wären zum einen die Postulierung von supersymmetrischen Teilchen mit hadronischem Charakter, welche einen höheren GZK-Cutoff Grenzwert besäßen. Oder zum anderen die Annahme, dass Neutrinos eine Masse besitzen, was die Neutrinos des „cosmic thermal relic neutriono Background“ und die Neutrinos mit einer Masse von eV die Z Bosonen Resonanz anregen ließe. Diese Z Bosonen zerfallen über Zwischenstufen in Elektronen, Neutrinos, Protonen und vor allem Photonen. Es wurde nun Vorgeschlagen, die so erzeugten Photonen und Nukleonen würden erst innerhalb der GZK Entfernungsgrenze( 100 Mpc) von der Erde produziert, was diesen Teil des Problems lösen würde. In diesem sogenannten „Z-Burst“ Szenario wäre der überwiegende Teil der erzeugten Teilchen Photonen – wie übrigens in „top-down“ Modellen im allgemeinen auch.
Ein anderer Vorschlag beinhaltet sogenannte metastabile-superschwere-relikt-Partikel (MSRP) mit einer Masse > GeV und einer mittleren Lebensdauer die größer ist als das Alter unseres Universums. Ein Teilchen mit diesen Eigenschaften läge außerhalb des Standardmodells und würde vermutlich aus sogenanten „topologischen Defekten“ im Universum(z.B. : magnetische Monopole oder kosmische Strings) stammen. In diesem Fall würde der GZK-Cutoff komplett entfallen.

Abbildung 20 Die Bahnen von geladenene und ungeladenen Teilchen der kosmischen Strahlung

Während der ungeladene Teil der kosmischen Strahlung sich annähernd geradlinig im Kosmos ausbreitet, wird der elektrisch geladene Teil der Strahlung von intergalaktischen Magnetfeldern homogener und irregulärer Natur abgelenkt und verliert daher auf der Reise durch das Weltall jegliche Richtungsinformation. Dieser Einfluss tritt logischerweise auch in unmittelbarer Erdnähe auf. Wie eingangs bereits beschrieben, werden Teilchen niederer Energien vom Erdmagnetfeld zu den Polen hin abgelenkt oder sogar in den Strahlungsgürteln in „Magnetischen –Flaschen“ gefangen. Aufgrund all dieser chaotischen Beeinflussungen der Bahnen geladener Teilchen ist es nicht verwunderlich, dass die geladene Komponente der kosmischen Strahlung bis zu Energien von E= eV annähernd isotrop, gleichmäßig über den Himmel verteilt, eintrifft, während die ungeladene Komponente immer eindeutig aus der Richtung ihrer Quellen einfällt uns somit auf diese zeigt. Bei höheren Energien sind die richtungsverändernden Einflüsse der Magnetfelder geringer, was zu minimalen Anisotropien führt. Beim Eintritt in das Sonnensystem gerät die kosmische Strahlung in Wechselwirkung mit dem von der Sonne gestreuten interplanetaren Magnetfeld und dem Sonnenwind ( der Heliosphäre). Daher ändert sich die Intensität der Strahlung mit zwei Perioden : einem 27-tägigem Zyklus wegen der Sonnenrotation und einem 11-jährigem Zyklus wegen der Sonnenaktivität. Desweiteren hat die Heliopshäre einen abschirmenden Effekt auf geladene Teilchen geringer Energie extragalaktischen Ursprungs. Die Teilchen des Sonnenwindes selbst besitzen im Vergleich zur kosmischen Strahlung weitaus geringere Energien und werden daher bei den Betrachtungen der hochenergetischen Strahlung nicht weiter beachtet. Für die Strahlungsgürtel der Erde aber sind besonders die Teilchen des Sonnenwindes relevant. Aufgrund all dessen wird schnell klar, dass nur die nicht geladene Komponente der kosmischen Strahlung oder aber die EHE-Teilchen der geladenen Komponente für die Beobachtung der Quellen interessant sind.

Beim Betrachten der Häufigkeit, mit der sehr energiereiche Partikel der kosmischen Strahlung wird schnell klar, dass eine direkte Beobachtung der primären Teilchen quasi unmöglich ist. Der überwiegende Teil der Primärteilchen der kosmischen Stralung erreicht die Erdoberfläche auch gar nicht. Lediglich die Teilchenschauer, welche durch die Wechselwirkungen des Primärteilchens in der Atmosphäre hervorgerufen wurden sind auf der Erdoberfläche messbar.

3.3 Sekundäre kosmische Strahlung / Airshower :

Abbildung 21 künslerische Impression eines Luftschauers

Die primäre kosmische Strahlung wird durch Wechselwirkungen auf dem letzten Teil der Reise mit den Atomkernen der atmosphärischen Luft stark modifiziert was zu den sogenannten Luftschauern , auch „Teilchenkaskaden“ genannt, führt. So geht das Ursprungsteilchen unter Umständen bei der Wechselwirkung verloren, durch die Anzahl und Energie der erzeugten Sekundärteilchen lässt sich jedoch relativ genau rekonstruieren welche Energie das Teilchen besaß und um welche Teilchenart es sich handelt.

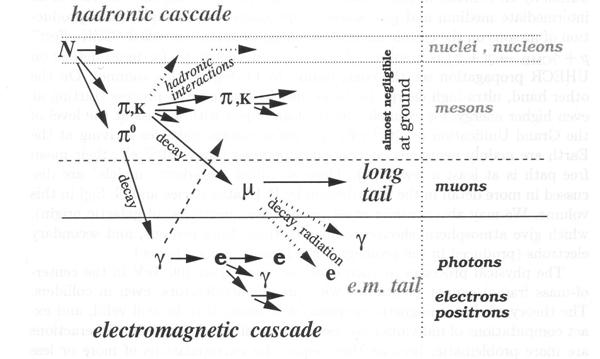
Abbildung 22 Teilchenkaskade eines Primärteilchens der kosmischen Strahlung

Zunächst soll die durch geladenen Partikel ausgelöste Kaskade betrachtet werden. Dabei ist diese für ein einfallenes Nukleon mit der Massenzahl A (, da Kerne größer als Eisen praktisch nicht auftreten ), die erste Wechselwirkung, welche meist in der oberen Atmosphäre in Höhen von etwa 20 km auftritt, hadronisch. Näherungsweise ist ein Kern A der Energie E äquivalent zu der Superposition von A unabhängigen Kernen mit der Energie.
Die Eindringtiefe X in die Atmosphäre wird üblicherweise in g/cm² angegeben.Dieser Quotient aus Länge und Dichte ist materialspeziefisch aber unabhängig von anderen Größen wie Aggregarzustand, Temperatur und Druck. Die Massenbelegung der Atmosphäre entspricht normalerweise 1000 g/cm², was einem Luftdruck von 1000 hPa entspricht.
Die Strahlungslänge für Photonen und Elektronen in Luft () und dieWechselwirkungslänge für Hadronen() entsprechen nur Bruchteilen der Atmosphäre, weshalb von der primären kosmischen Strahlung praktisch nichts auf den Erdboden erreicht.

Die primären Wechselwirkungen produzieren neben den an der Wechselwirkung beteiligten Teilchen eine große Anzahl sekundärer Partikel, vor allem Pionen und Kaonen , welche wiederum zerfallen oder erneut in der Luft wechselwirken, was die hadronische Kaskade am laufen hält. Neutrale Pionen zerfallen (außer bei sehr hohen Energien der Primärteilchen im EeV Bereich) in Photonen ehe sie erneut wechselwirken können( ) , sodass bei jeder Stufe der hadronischen Kaskade 1/3 der Energie in Photonen transferiert wird, was die elektromagnetische Komponente des Schauers erzeugt. Die Photonen produzieren Paare. Diese ihrerseits hochenergetischen Elektronen emititeren Photonen als Bremsstrahlung in den Coulombfeldern der Atmosphärenatome. Sich anihilierende Paare erzeugen ebenfalls Photonen. Ein kleiner Bruchteil der elektromagnetischen Komponente wird in die hadronische Komponente zurückgeführt, weshalb auch durch primäre Photonen injizierte Schauer unter Umständen eine hadronische Komponente entwickeln können.

Die hadronische Kaskade (ein paar vereinzelte Kerne ausgenommen) endet mit einem Zerfall der geladenen Pionen in Myonen und Neutrinos (in mittleren Höhen bei etwa 6 km mit einer großen Streuung). (, ) Ein Großteil der Myonen erreicht den Erdboden bevor sie zerfallen ohne einen nennenswerten Energieverlust. Myonen besitzen einen sehr kleinen Wirkungsquerschnitt, weshalb sie ein sehr gutes Durchdringungsvermögen besitzen, sind aber aufgrund ihrer Ladung relativ einfach nachzuweisen, weshalb man sie auch die „durchdringende Komponente“ der kosmischen Strahlung nennt.
Die elektromagnetische Kaskade setzt sich fort bis zu Energien unter 1 MeV, bei denen Elektronen weiter abgebremst werden ohne dabei Bremsstrahlung zu emmitieren. Außer bei sehr steil einfallenden Schauern ist dies auf Meereshöhe noch nicht der Fall. Die elektromagnetische Kaskade erreicht fasst nie Meereshöhe, sie haben ein Schauermaximum in ca. 10 km Höhe. Die beim Zerfall der geladenen Pionen entstehenden Neutrinos haben einen so kleinen Wechselwirkungsquerschnitt, das sie ungehindert durch die Atmosphäre und einen großen Teil der Erde, bei niederen Energiene sogar weit darüber hinaus, propagieren. Aufgrund dessen lassen sich diese auch nur recht schwierig nachweisen.

Bei höheren Energien lässt sich die Anzahl der geladenen Partikel eines Schauers durch die Gaisser-Hillas-Funktion [R 5] in Abhängigkleit von der Tiefe des Schauers X ausdrücken :

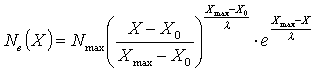(3.3.1)

Wobei die Tiefe bei der die erste Wechselwirkung stattfand, darstellt und die Wechselwirkungslänge von der Natur des Primärteilchens abhängt. ist die Tiefe des Maximums von . steigt linear mit der Energie des Primärteilchens, wohingegen linear zum Logarithmus dieser Energie variiert.

Sollte das Primärteilchen ein Photon oder Electron sein, so sind die ersten Schritte der Kaskade nur elektromagnetisch und die Abnahme der Energie geringer als bei deiner hadronischen Kaskade – daher ist größer in einem Proton- bzw. Nukleonschauer

Die physikalischen Prozesse in einer Teilchenkaskade liefern für gewöhnlich moderate Transversalimpulse, unabhängig von der Energie. Die meisten hochenergetischen Teilchen sind um die ursprüngliche Schauerachse herum zu finden, sie bilden den „Kern“ des Schauers. Photonen und Elektronen, sowie Myonen niedrigerer Energie sind wesentlich weiter von der Schauerachse verbreitet. Dieser „elektromganetische Schein“ hat eine nachweisbare Dichte noch in einigen Kilometern Entfernung. Der elektromagnetische Teil dieses „halo“ erhöht sich mit zunehmender Eindringtiefe so lange der „Kern“ aktiv ist, erreicht dann bei ein Maximum und nimmt danach rapide ab. Bei ist er so gut wie verschwunden. Die meisten Myonen „reisen“ weiter als die elektromagnetische Kaskade und bilden somit einen „myonischen Schweif“ mit einer zunehmenden Ausbreitung .

Auf Meereshöhe bilden Myonen ganz klar die dominierende Komponente der geladenen Partikel eines Teilchenschauers. Da diese wie oben beschrieben überwiegend aus Pionenzerfällen stammen, lässt sich das Myonensprektrum auf Meereshöhe also direkt aus dem Pionenquellspektrum mit einigen Modifikationen herleiten. Bei unterschiedlichen Energien, speziell in Randbereichen, ändert sich die Zerfallslänge der Pionen, wobei Pionen > 100 GeV zunächst tertiäre Pionen erzeugen, die zwar in Myonen zerfallen, dann aber Myonen geringerer Energie leifern. Zudem ist die Intensität der Myonen noch vom Zenitwinkel abhängig. Beachtet man all diese Aspekte lassen sich anhand der am Boden gemessenen Myonen auf das Primärteilchen Rückschlüsse ziehen. Die Richtung des Primärteilchens lässt sich beinahe direkt dem Schauer entnehmen. Masse und Energie jedoch nur indirekt aus den Messdaten bestimmen. So kann man anhand von in Teilchenbeschleunigern gewonnenen Erkentnissen über die Wechselwirkungen der Teilchen Schauer eines bestimmten Teilchens am Rechner simulieren und dann die gemessenen Werte damit vergleichen. Ein Beispiel hierfür ist das Luftschauersimulationsprogramm CORSIKA (COsmic Ray SImulations for KAscade), welches unter anderem zeigt, dass hochenergetische Hadronen in einem relativ engen Radius (~30m) um die Schauerachse konzentriert sind, die Photonen und Myonen jedoch teilweise bis zu 100m entfernt niedergehen können.

Die Anzahl der Myonen steigt bei fester Gesamtenergie nur geringfügig mit der Masse des Primärteilchens und erlaubt daher eine erste Abschätzung seiner Energie. Die am Erdboden beobachtete Elektronen- und insbesondere auch die Hadronenzahl sinkt dagegen mit zunehmender Masse des Primärteilchens. Schwerere Atomkerne haben eine kleinere Wechselwirkungslänge in Luft, dies führt zu einer früheren Entwicklung des Schauers und damit zu einer stärkeren Absorption der elektromagnetischen und hadronischen Komponente des Schauers in der Atmosphäre. Das Verhältnis der Elektron- oder Hadronzahl relativ zur Myonzahl ermöglicht somit eine Abschätzung der Masse des Primärteilchens. Ergänzende Messgrößen sind die Formen der Lateralverteilungen der jeweiligen Teilchensorten, die Höhe des Schauermaximums, die rekonstruierten Myon-Produktionshöhen, die Struktur des hadronischen Schauerkerns und das Zeitprofil der Schauerfront.

Bei den oben angegebenen Wechselwirkungslängen und einer Massenbelegung der Atmosphäre von 1000 g/cm² erhält man auf Meereshöhe 80% Photonen, 18% Elektronen und Positronen, 1,7% Myonen und 0,3% Hadronen. Bei mittleren Energien der Primärteilchen ist der Fluss der kosmischen Strahlung jedoch so groß, dass ein mehr oder minder gleichmäßiger Fluss von Sekundärteilchen vorliegt, der eine Rekonstruktion einzelner Schauer bei diesen Energien unmöglich macht.

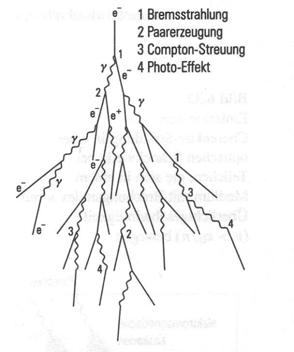
Abbildung 23 Die elektromagnetische Kaskade

Für ein einfallendes Photon sind zunächst nur elektromagnetische Wechselwirkungen relevant. Die Prozesse Bremsstrahlung, Ionisation, Comptoneffekt, Paarerzeugung und Photoeffekt spielen hier eine Rolle. Da diese Prozesse immer wechselseitig Paare, Elektronen und Photonen erzeugen, ist es quasi unmöglich festzustellen, ob ein Elektron oder ein Photon den Schauer initiiert hat. Ab Energien von 10 TeV erreichen diese Schauer gelegentlich die Erdoberfläche (z.B. auf Bergen), die laterale Ausbreitung ist eher gering. Bei hohen Energien herscht der Paarbildungsprozess eindeutig vor, bei kleinen Energien der Photoeffekt sowie die Ionisation.

Compton Effekt :

Photoeffekt :

Paarblidung :

Bremsstrahlung :

Ionisation

Alle Prozesse sind selbstverständlich auch bei Positronen denkbar !

3.4 Luftfluoreszenz

Als Nebeneffekt wird der in der Atmosphäre vorhandene Stickstoff, welcher 78% der Luft ausmacht, durch die Schauerteilchen zum Leuchten angeregt und emmitiert ein blau-ultravioletes Floureszenzlicht. Bei Energien größer als eV ist diese diffuse Strahlung gegenüber dem Hintergrund des Sternlichts intensiv genug, um auf Meereshöhe im Wellenlängenbereich von 290 nm – 440 nm abgrenzbar zu sein. Da dieses „Licht“ isotrop ist, kann ein Schauer damit aus jeder Richtung beobachtet werden.

3.5 Cherenkovstrahlung

Abbildung 24 Modelldarstellung der optischen Schockwelle eines mit "Überlichtgeschwindigkeit" propagierenden Teilchens

Wenn geladene Teilchen durch ein Medium mit einer Geschwindigkeit größer als die Lichtgeschwindigkeit in diesem Medium, propagieren, wird sogenannte Čerenkov-Strahlung emmitiert. [R 6]

, somit ist : . (3.5.1)

Die geladenen Partikel polarisieren die Moleküle des Mediums, welche promt wieder in ihren Grundzustand zurückkehren und bei diesem Sprung spontan Photonen emittieren. Das Teilchen, was mit durch die Atmosphäre fliegt, sendet kontinuierlich Čerenkovlicht mit Geschwindigkeit c aus. Da n aber sehr nahe bei 1 liegt, ist und somit bewegt sich jedes Čerenkovphoton genau so schnell wie das Teilchen selbst. Die Čerenkovphotonen kommen dann alle etwa gleichzeitig beib Beobachter an, auch wenn die Emmmision lang war, was bewirkt, dass das Čerenkovlicht in Wirklich keit nur ein sehr kurzer Lichtblitz ist. Die Erzeugung von Čerenkov-Strahlung in einer optischen Schockwelle ist das optische Analogon zu den bei Überschallgeschwindigkeiten auftretenden Schockwellen. Das Licht wird näherungsweise immer unter einem bestimmten Winkel emittiert.

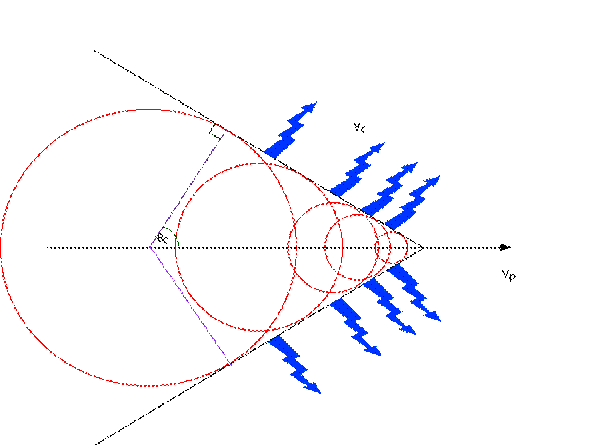
Abbildung 25 Modelldarstellung des Cherenkoveffektes

Es gilt , daher ist . (3.5.2)

Die Schwellenwertenergie für den Vorgang, welche sich aus der Schwellenwertbedingung für die Geschwindigkeit ableitet lautet :

, (3.5.3)

da : . (3.5.4)

Die Anzahl der Čerenkovphotonen, die je Weglänge dx emittiert werden, lässt sich für den Brechungsindex n(λ) > 1 beschreiben durch :

, (3.5.5)

wobei Z die Ladung des Teilchens beschreibt, α die Feinstrukturkonstante und λ die Wellenlänge darstellt. Im Spektralbereich des sichtbaren Lichtes wären dies (ein von λ unabhängiges n angenommen) :

, bei .

Daraus erkennt man leicht, das es sich hierbei zwar um ein relativ starkes Signal handelt ( bei einigen km Weglänge), dieses sich jedoch auf einem Kreis von rund 100m Radius ausbreitet, weswegen mit Teleskopen nur wenige Photonen eingefangen werden können. Stellt man das differentielle Spektrum der Čerenkovstrahlung, welches nach (3.5.5) beschrieben ist durch :

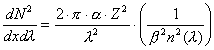, (3.5.6)

dar, so erkennt man ein Maxium bei etwa 330 nm. Daraus wird ersichtlich, dass die Mehrzahl der Čerenkovphotonen im ultravioletten Bereich liegen muss , da gilt.

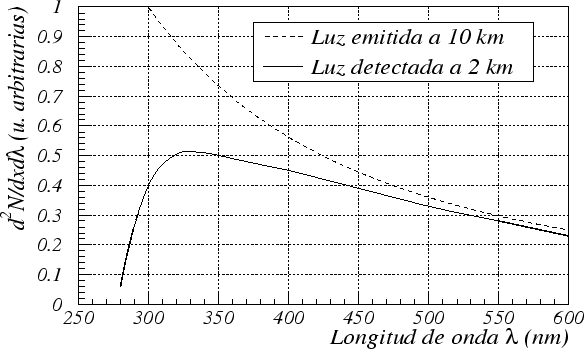
Abbildung 26 Das diferrentielle Čerenkovspektrum in einer Höhe von 10 km (gestrichelt) und 2km (durchgezogen).

Doch selbst in komplett abgedunkelten Flüssigkeitsdetektoren hat man mit einem niedrigen“Quanten-Wirkungsgrad“ (nur etwa 20% der Čerenkovphotonen) und einem Fehler zu kämpfen, der entsteht, da n eben doch von λ abhängig ist, wodurch sich die Anzahl der detektierbaren Photonen nochmals verringert. Im Röntgenstrahlbereich werden keine Čerenkovphotonen emittiert, da hier gilt.
Für die Entdeckung und Erklärung des Effektes erhielt Pavel Alekseyevich Čerenkov 1958 1/3 des Physiknobelpreises.

4. Messverfahren

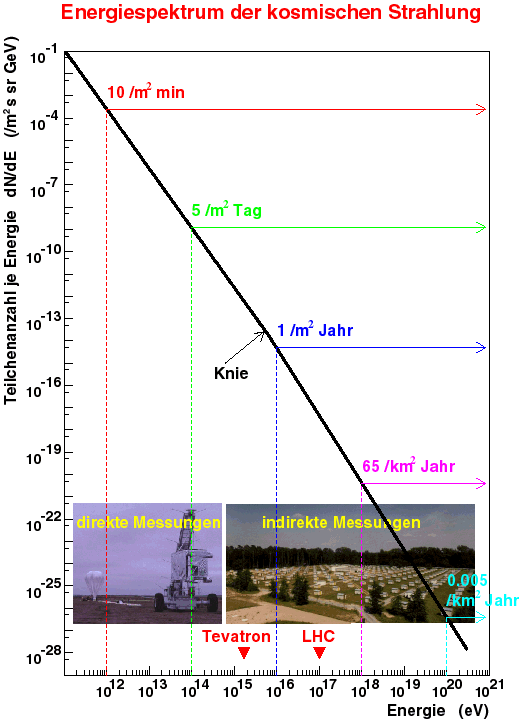
Abbildung 27 Das Energiespektrum der kosmischen Strahlung auf der Erde und die korespondierenden Messverfahren

Der Teilchenfluss der kosmischen Strahlung hängt über ein Potenzgesetz von der Energie ab. () . Daher wird wird der Fluss bei höheren Energien sehr klein. Somit sind bei verschiedenen Energien sehr unterschiedliche Messverfahren geeignet.

Für gringe Energien bis eV können direkte Messungen durch Ballon- oder Satellitenexperimente durchgeführt werden. Um die geladene kosmische Strahlung messen zu können, benutzte man anfangs die in der historischen Einleitung bereits erwähnten Ionisationskammern als Nachweisgerät. Heute kommen hier jedoch komplizierte Apparaturen zum Einsatz. Die Höhe muss durch Satelliten oder Ballons, welche bis zu 40 km hoch steigen können, gewährleiset werden, da die Primärteilchen wie eben beschrieben in der Atmosphäre bereits in oberen Luftschichten in Wechslwirkung treten und Teilchenschauer initiieren. Bei einer Teilchenenergie von eV beträgt der Fluss jedoch nur noch 1 Teilchen pro m² pro Jahr. Solch ein geringer Fluss lässt sich nicht mehr direkt mit Satelliten- oder Ballondetektoren nachweisen, da die in diesen Geräten realisierbaren Kollektorflächen hierfür viel zu klein sind. Somit ist den direkten Messungen hier eine natürliche Grenze gesetzt.

4.1 direkte Messungen : Ballon / Satellitenexperimente

Abbildung 28 Das ISOMAX als Beispiel für ein (relativ) aktuelles Ballonexperiment.

Bei Experimenten, die auf die direkte Bestimmung der kosmischen Strahlung ausgelegt sind, kommen verschiedene auf die jeweiligen Teilchentypen spezialisierte Messapparaturen zum Einsatz. Typischerweise werden Magnetspektrographen(Massenspektrographen) zur Masse- und Impulsbestimmung, Szintillationszähler, Aerogel-Cherenkovzähler und Flugzeitmesser zur Bestimmung der Ladung und Geschwindigkeit eingesetzt.

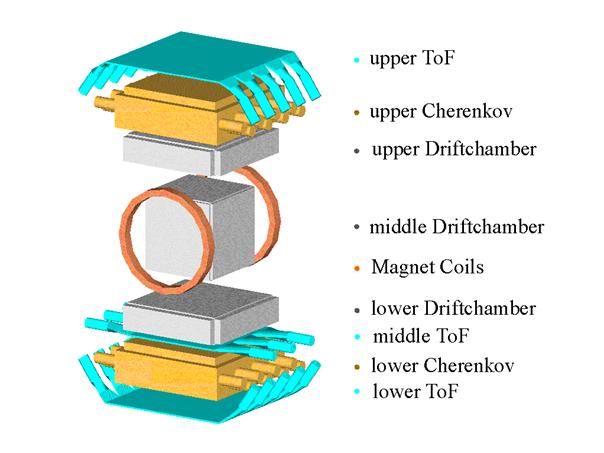
Abbildung 29 Schematischer Aufbau des ISOMAX Experiment : In der Mitte die zwei Magnetfeldspulen des Massenspektrographen, In dunklem Gelb die beiden Ĉerenkovzähler und in hellblau die Flugzeitmesser (ToF = Time of Flight)

Während bei niedrigen Energien Ballonflüge eine sehr preiswerte Version von direkten Messungen ermöglichen, müssen bei höheren Energien Satelliten als Träger für die Messapparaturen eingesetzt werden, da der Teilchenfluss bereits so gering ist, dass innerhalb der möglichen Flugzeiten der Ballone nicht mehr genügend Teilchen gemessen werden können.

Auch wenn die geladenen Partikel im unteren Bereich des Spektrums leider keine Richtugsinformationen liefern, so lassen sich hier doch wertvolle Eigenschaften der kosmischen Strahlung ermitteln. So ist hier eine genaue Bestimung der Art des Teilchens möglich. Die bereits erwähnte Zusammensetzung der geladenen Komponennte sowie die Messungen der Elementhäufigkeiten gehen auf direkte Messungen, wie zum Beispiel beim Ballonexperiment ALICE, zurück.

Desweiteren werden auf direkten Messungen basierende Experimente zur Messung von Antimaterie in der kosmischen Strahlung, zur detailierten Energiespektrumsbestimmung und zur Bestimmung des Isotopenverhälnisses durchgeführt. So gelang mit dem Ballonexperiment IMAX der Nachweis von Antiprotonen in der kosmischen Strahlung.

4.2 Koinzidenzzählung (Auger, Kaskade)

Da direkte Messmethoden schon seit einiger Zeit zur Verfügung stehen und auch sehr konkrete Informationen liefern, ist der Spektralbereich bis eV realtiv gut „vermesen“ und analysiert, auch wenn dazu auch heute noch Experimente durchgeführt werden. Bei höheren Energien gestaltet sich die Messung, vor allem aber die Bestimmung von Masse und Art des Primärteilchens, wie bereits bei der Erklärung der Teilchenschauer erwähnt, wesentlich schwieriger. Dementsprechend übersichtlich ist auch die heute vorliegende Anzahl von Messdaten.

4.3 Kascade

Abbildung 30 Das Kascade Experiment in Karlsruhe

Aufgrund des geringen Teilchenflusses bei höheren Energien können nur durch breitflächige Felder von Detektoren zum Nachweis der Teilchenschauer eines Primärteilchns genutzt werden. Hierfür können Szintillationszähler zum Einsatz kommen.Ein Beispiel hierfür wäre das „Karlsruhe Shower Core and Array Detektor“ (Kascade), ein 200x200 m² großes Feld von 252 Szintillationszählern, die im Abstand von 13m postiert sind und die Photonen, Elektronen und Myonen einer Teilchenkaskade messen können. Ergänzt wird die Anlage durch ein Zentraldetektor, der in der Mitte des Arrays lokalisiert ist und als Hauptbestandteil ein 16 x 20 m² großes Hadronkalorimeter beinhaltet. Vor kurzem wurde das Multidetektor Array Kascade durch ein 37 Szintilationszähler umfassendes, 700 x 700 m² großes Array „Grande“ ergänzt. Dieses erweiterte Experiment wird „Kascade Grande“ genannt und erlaubt umfassende Messungen der kosmischen Strahlung im Energiebereich von 0,1 PeV – 1,0 EeV, was eine vollständige Untersuchung des „Knie“-Bereiches des Spektrums ermöglicht.
Hierbei versucht man so viele Luftschauer wie möglich zu beobachten, um das dreigeteilte Problem der Bestimmung Primärenergie, der Ermittlung der Masse des Primärteilchens und dem Verständniss der hadronischen Wechselwirkungsmechanismen in der Atmosphäre besser lösen zu können. Zusätzlich kann man die Gültigkeit der Hadronenwechselwirkungsmodelle, welche bei den CORSIKA Monte Carlo Simulationen vonLuftschauern zum Einsatz kommen, testen. Hierzu misst man Kenngrößen wie den Einfallswinkel, die Position der Schauerkernachse und die Gesamtzahl der geladenen Partikel.
Im Moment untersucht man die dominierende Teilchenart in der Knieregion. Es scheint als ob hier ein Übergang von Protonen zu Eisenkernen als Hauptbestandteil der geladenen Komponente stattfindet.

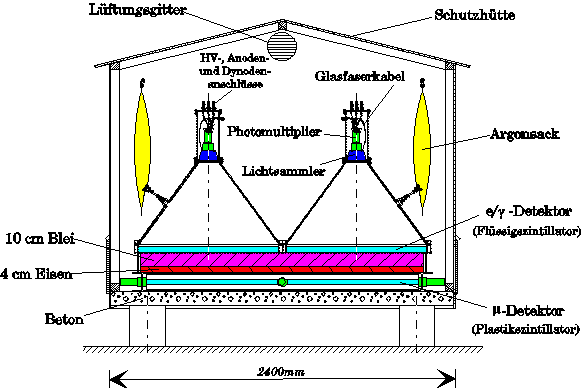
Abbildung 31 Querschnitt einer der 252 Detektorstationen des KASCADE-Projektes

4.4 Fly’s Eye / HiRES

Abbildung 32 Das Fly's Eye Teleskop in Utah, USA

Bereits 1967 schlug A. Bunner vor, dass diffuse Stickstoff-Floureszenzlicht für Messungen der kosmischen Teilchenstrahlungen zu verwenden.[R 7] Dieses Experiment wurde im Fly’s Eye Detektor in Dugway, Utah in den USA realisiert. Der Detektor besteht aus zwei Arrays von Parabolspiegeln, die jeweils 1,5 m Durchmesser haben und mit einer Matrix von 12 oder 14 Photomultipliern ausgestattet sind. Die Spiegel sind alle anders gerichtet, um so den gesamten Nachthimmel abdecken zu können. Jedes Array zeichnet den Himmel auf, wobei eine Photoröhre einen Pixel auf der Himmelskarte repräsentiert.
Indem man das atmosphärische Fluoreszenslicht in Abhängigkeit von der Zeit aufnimmt, während der Teilchenschauer über das Detektorfeld zieht, kann die Schauerbahn rekonstruiert werden. Wenn die Distanz und Orientirung der Linienquelle einmal bekannt ist, kann das Signal von jedem Photomultiplier in eine Energie, die in diesem Bahnabschnit abgestrahlt wurde, konvertiert werden.
So kann die Einfallsrichtung, die Energie und die Art des Teilchens der kosmischen Strahlung bestimmt werden. Schauerbahnen nahe dem Detektor können nicht analysiert werden, da das Čerenkovlicht, welches in Luft im Winkel von der Schauerachse emittiert wird, die sehr schwache isotrope Fluoreszensstrahlung überdeckt Daher funktioniert diese Apparatur auch nur bei sehr klaren, mondlosen Nächten, da das Szintillationslicht sonst nicht mehr im Hintergrund auszumachen ist. Das Fly’s Eye Team beschreibt es treffend mit dem Vergleich die Photonen einer blauen 5W Glühbirne, die in mehreren km Entfernung durch die Atmosphäre fliegt, zu messen.

Abbildung 33 Einer der Spiegel des Fly's Eye Telekopes

Das 1991 beendete Fly’s Eye Projekt fand in HiRES einen würdigen Nachfolger, welches ein weiteres, größeres Array von Fluoreszensdetektoren darstellt. Besonderes Ziel ist die Suche nach Partikeln der kosmischen Strahlung, welche Energien jenseits des GZK-Cutoff besitzen. So ist bereits 1991 der Nachweis eines leichten Teilchens, vermutlich eines Protons, mit einer Energie von 3.5 x 10²⁰eV (oder 56J) gelungen.

4.5 Auger Obervatorium

Abbildung 34 Eine der 1600 Detektorstationen des Auger Observatoriums

Das Pierre Auger Observatorium ist ein Beispiel für die Messung von ausgedehnten Luftschauern in der argentinischen Pampa. Hierbei handelt es sich um ein Array von mehreren 100 der geplanten 1600 Detektorenstationen im Abstand von jeweils 1,5 km, in denen das Čerenkovlicht eines Schauerteilchens in einem Wassertank mit Photomultipliern nachgewiesen wird. Zusätzlich sind bereits 2 der geplanten 4 Fluoreszenslichtdetektorstationen (mit jeweils 6 Fluoreszensteleskopen) mit einer Winkelauflösung von 1,4 ° ins System integriert, um zusätzliche Schauerdaten messen zu können. Nach Vollendung wird der Detektor eine Fläche von 3000 m² abdecken und man hofft, etwa 30 Schauererignisse von Energien > eV pro Jahr messen zu können. Um auch den Nordhimmel abdecken zu können soll eine ähnliche Anlage im Rahmen des Auger Projektes auf der Nordhalbkugel errichtet werden.

Abbildung 35 Einer der zentralen Fuoreszensdetektoren des Auger-Teleskopes

Abbildung 36 Zeichnung eines Teilchenschauers über dem Augerteleskop

4.6 Čerenkovdetektoren

Eine weitere Methode der Messung ist das Beobachten der Čerenkovstrahlung, welches von den Schauerteilchen emittiert wird. Diese Technik wird vor allem zur Messung von Gammaquanten und Neutrinos kosmischer Herkunft eingesetzt. Bei den Neutrinos ist es oft das Myon , in welches sich ein Myonneutrino() bei Wechselwirkung verwandelt, das in einem Detektor nachgewiesen wird

Abbildung 37 Panoramaansicht des AMANDA-II Areals

Ein Beispiel für einen Detektor für kosmische Neutrinos ist AMANDA II. Ein Projekt in der Antarktis, bei dem die Čerenkovstrahlung der Neutrinos im Eis durch ungefähr 677 kugelförmige „Optische Einheiten“ mit jeweils 8 Photomultipliern gemessen wird, die an 19 Leinen ins Eis eingelassen sind. Im arktischen Eis bilden sie in einer Tiefe von 1500m bis 2000m, wo das Eis glasklar und absolut dunkel ist. einen annähernd zylindrischen Detektor mit einem Radius von 100m.

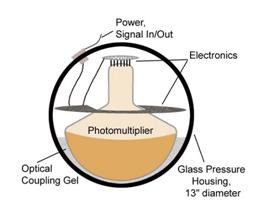
Abbildung 38 Eine der Optical Units des AMANDA Detektors

Man nutzt hierbei die gesamte Erde als Abschirmung für solare und irdische Neutrinos (z.B. aus Luftschauern) um die Neutrinoereignisse des Nordhimmels beobachten zu können. Da die Erde für Neutrinos mit einer Energie > 1 PeV undurchsichtig wird, versucht man Neutrinos, die von oben (Südhimmel) kommen, zu beobachten, da bei solchen Energien der Untergrund durch atmosphärische Neutrinos klein ist (und stark fällt). Bis heute ist es nicht eindeutig gelungen, auch nur ein kosmisches Neutrinoereignis zweifelsfrei zu messen.

Abbildung 39 Karte der im Jahre 2000 von AMANDA registrierten Neutrino-Ereignisse

Bis zum Jahre 2008 sollen im Rahmen von „IceCube“ 4800 Photomultiplier an 80 vertikalen Leinen rund um AMANDA II installiert werden, welche dann einen Detektorvolumen von 1 km³ abdecken werden. Mit diesem Experiment können Neutrinos mit Energien von bis zu eV gemessen werden, einem Energiebereich in dem das Universum für Gammastrahlung undurchsichtig ist und wo somit die Beobachtung von Neutrinos eine wichtige Rolle spielen kann. (Anm. V. Prof Lohse : Allerdings gibt aber die Abschwächung des Gammastrahlensignales eine direkte Methode der Messung des intergalaktischen Infrarotstrahlungsfeldes. Dies ist eine sehr wichtige kosmologische Größe.)

5. Beschleunigungsmechanismen :

Von Anfang an war die spannenste Frage der kosmischen Strahlung in welchen Objekten unseres Universums Teilchen auf solch hohe Energien beschleunigt werden können. Immerhin müssen hier Teilchenbeschleuniger am Werk sein, die um mal so große Endenergien erreichen, wie irdische Anlagen. Zunächst sollen einige vorgeschlagene Beschleunigungsmechanismen in Ansätzen erläutert werden um anschließend darzustellen, in welchen Bereichen des Universum diese vermutet werden.

Wie bereits bei der Beschreibung des Flussspektrums erwähnt, werden für verschiedene Energiebereiche unterschiedliche Mechanismen und somit meist auch unterschiedliche Quellen vermutet. Aufgrund der Form des Spektrums als auch der bisher gemessenen Maximalenergien lassen sich thermische Strahlungsquellen ausschließen. Vielmehr muss eine Verbindung von verschiedenen Mechanismen einzelne Partikel auf diese hohen Energien beschleunigen.

5.1 Fermibeschleunigung

Abbildung 40 Enrico Fermi

Bereits 1949 schlug Enrico Fremi [R 8] eine Beschleunigung von geladenen Partikeln durch wiederholte Kollisionen an diffusen Magnetwolken (magnetisiertem Plasma) als Beschleunigungsmechansimus vor. Erstaunlicherwiese wird hierbei ebenfalls ein Potenzspektrum erzeugt, das dem gemessenen erstaunlich nahe kommt.

Die Grundüberlegung hierbei ist, dass ein Teil der Energie des sich bewegenden Plasmas auf die einzelnen geladenen Partikel übertragen wird, indem die Energie des Teilchens jeweils um ein Vielfaches seiner Ausgangsenergie erhöht wird und so die nichtthermische Energieverteilung erreicht wird.

Angenommen ein Testpartikel erhöht seine Energie in einem Prozess bei jeder „Begenung“ proportional zu seiner Energie, so wäre die Energie nach n „Begenungen“ bei einer Energieänderung je Stoß gegeben durch :

(5.1)

wobei die Energie zum Zeitpunkt der Injektion in den Beschleuniger darstellt. Wenn die Wahrscheinlichkeit des Entweichens aus dem Beschleunigergebiet durch ausgedrückt ist, so lässt sich die Fluchtwahrscheinlichkeit nach n Stößen durch beschreiben. Die Anzahl n der zum Erreichen einer bestimmten Energie E nötigen Stöße ist, aus (5.1):

. (5.2)

Folglich ist der Anteil der Teilchen die auf Energien > E beschleunigt werden gegeben durch :

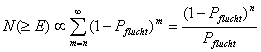. (5.3)

Durch Einsetzen von (5.2) in (5.3) erhält man :

, (5.4)

mit einem Spektralindex γ der sich ergibt durch :

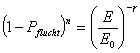
Hierbei wurde die Fluchtwahrscheinlichkeit ersetzt durch den Quotient von Beschleunigungszeit und der chrackteristischen Zeit des Verlassens der Beschleunigerregion . Nach einer verstrichenen Zeit t ist , daher gilt :

. (5.5)

Aus (5.5) wird offensichtlich, dass bei der Fermi-Beschleunigung hochenergetische Partikel länger zur Beschleunigung brauchen als Teilchen mit geringerer Energie. Würde von der Energie unabhängig sein, so würde sich bei einer maximalen Lebensdauer bei aus (5.5) auch eine Maximalenergie des Beschleunigers ergeben. In der Tat ist jedoch keinweswegs unabhängig von der Energie. In (5.4) wird der Potenzgesetzcharakter des Mechanismus offensichtlich, was zunächst formal mit dem des Spektrums nahekommt, wobei noch offen ist, inwiefern γ hier die gleichen Werte wie im Spektrum annimt.

5.2 Fermi Mechanismus verschiedener Ordnungen

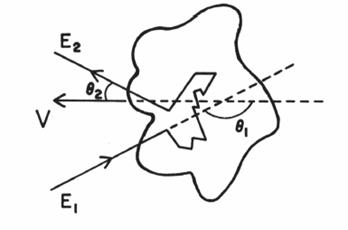
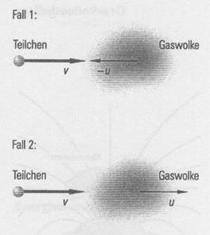
Abbildung 41 Beschleunigung durch eine Sich bewegende, teilionisierte Gaswolke

In der Abbildung tritt ein Testpartikel mit der Energie in die Gaswolke ein, wo es durch „Streuen“ an Irregularitäten des Magnetfeldes „diffundiert“. Als Ergebnis der Diffusion im Inneren der Wolke gleicht die Bewegung des Teilchens nach ein paar Streuungen der durchschnittlichen Bewegung der Gaswolke. Im Ruhesystem des Gases hat das Teilchen dann eine Gesamtenergie ( Restmasse + kinetische Energie ) von :

, (5.6)

mit und dem Lorentz-Faktor.

Alle „Streuungen“ in der Wolke passieren aufgrund der Bewegung des Magnetfeldes und sind daher total elastisch. Daher ist die Energie des Teilchens beim Verlassen des Beschleunigers im bewegten Bezugssystem gegeben durch: . Diese Energie zurück ins Laborsystem übertragen stellt dann die Energie des Teilchens nach der Begegnung mit der Magnetwolke dar :

. (5.7)

Setzt man (5.6) in (5.7) ein so ergibt sich als Energieänderung :

(5.8)

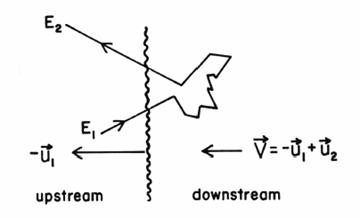
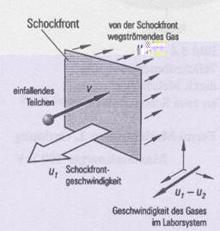
Abbildung 42 Beschleunigung an einer ebenen Schockfront

Die andere denkbare Situation ist in der Abbildung illustriert. Hier bewegt sich eine große, ebene Schockfront mit der Geschwindigkeit . Das geschockte Gas fließt von der Schockfront mit der Geschwindigkeit relativ zur Ebene weg, wobei gilt. Im Laborsystem jedoch, bewegt sich das Gas hinter dem Schock mit der Geschwindigkeit . Gleichung (5.8), welche für die Begegung mit diffusen Gaswolken hergeleitet wurde, gillt auch hier, wobei jetzt als Geschwindigkeit des geschockten Gases („downstream“) relativ zum ungeschockten Gas („upstream“) interpretiert wird.

Der wesentliche Unterschied zwischen den beiden Fällen offenbart sich beim Betrachten der Durchschnittswinkel zur Erlangung des durchschnittlichen Teilenergiegewinn pro „Begegnung“, aus den Gleichungen (5.1) bis (5.5).

5.3.1 Fermi Mechanismus zweiter Ordnung

Da die Bewegung des Testpartikels in der Wolke zufällig erfolgt, treten alle Winkel mit der gleichen Wahrscheinlichkeit auf, weshalb gilt. Aufgrund der Bewegung der Wolke, ist die Wahrscheinlichkeit das der Partikel mit in die Wolke eintritt, bei einem relativistischem Teilchen und einer langsamen Wolkenbewegung, proportional zu , weshalb sich ergibt.Somit gilt für die Begegnung mit einer Gaswolke :

. (5.9)

5.3.2 Fermi Mechanismus erster Ordnung

Da der Schock eine Ebene darstellt, ist die Wahrscheinlichkeit das der Partikel die Ebene mit trifft, proportional zu , weshalb sich ergibt. Somit gilt gleiches auch für den Austrittsinkel : und es rgibt sich :

. (5.10)

Bei diesen Betrachtungen wird als „Begegnung“ jeweils ein Paar von Ein- und Ausritt in die Wolke bzw. Vorwärts- und Rückwärtsdurchquerung der Schockfront angenommen. Beim „originalen“ Fermimechanismus zweiter Ordnung, können die Partikel entweder einen Verlust oder einen Zuwachs an Energie verbuchen. Nach vielen Begenungen stellt sich jedoch ein Energiegewinn ein. Dieser fällt hierbei sehr klein aus, weshalb eine sehr langer Zeitraum zur Beschleunigung auf sehr hohe Energien nötig ist. Bei Begegnungen mit Schockfronten stellt sich hingegen aufgrund der Geometrie der unendlichen Ebene immer ein Energiegewinn ein. Die Ordnung ist gegeben durch den Exponenten der Geschwindigkeit der Plasmabewegung. Für diesen Beschleunigungsmechanismus ist eine minimale Injektionsenergie nötig, welche durch andere Verfahren geliefert werden muss.

Beim orginalen Fermimechanismus ist die Beschleunigungsregion die galaktische Scheibe, daher ist . Die Beschleunigungsrate ist die Rate der Kollisionen der kosmischen Strahlung mit der Geschwindigkeit c mit Wolken, welche durch eine räumliche Dichte und einen Wirkungsquerschnitt beschrieben ist. Daher ist . Der intergrale Spektralindex ist somit gegeben durch :

. (5.11)

Beim Mechanismus erster Ordnung, der Begegnung mit einer großen, ebenen Schockfront, ist die Begegnungsrate gegben durch eine Projektion des isotropen Flusses der kosmischen Strahlung auf die ebene Schockfront :

wobei die Anzahldichte der gerade beschleugten Partikel darstellt.Die Ausbreitungsrate des Flusses von der Schockfront(„downstream“) ist gegeben durch : , somit gilt für die Fluchtwahrscheinlichkeit :

(5.12)

Somit gilt für den Index bei der Beschleunigung an einer Schockfront :

. (5.13)

Im Vergleich zum Fermimechanismus zweiter Ordnung ist der Spektralindex hier unabhängig von der absoluten Geschwindigkeit des Plasma (V). Es hängt lediglich vom Quotienten der down- und upstream Geschwindigkeiten diesseits und jenseits der Schockfront ab. In diesem Fall lässt sich ein Spektralindex von γ=2 vorraussagen.

Dies kommt dem gemessenen Spektrum der kosmischen Strahlung zwar nahe, wiest aber eine nicht unerhebliche Diskrepanz auf. Im gemessenen Flussspektrum gilt γ = 2,7 für Energien bis eV, danach ist γ = 3, um bei eV wieder zu γ = 2,7 abzuflachen.[1]

6. Potentielle Quellen der kosmischen Strahlung :

6.1 Schockwellen durch Supernovaüberreste

Eine interstellare Gaswolke kann unter dem Einfluss ihrer eigenen Gravitation kollabieren, wenn sie eine dem Jeanschen Kriterium genügende Masse besitzt, also erfüllt ist. Diese Kontraktion, welche einige Millionen Jahre in Anspruch nimmt, käme niemals zum Stillstand, würde sich das Gas nicht durch die abnehmende potentielle Gravitationsenergie und deren Umwandlung in innere Energie gewaltig aufheizen. Bei Temperaturen von über 10 Millionen Kelvin stellt sich der Prozess der thermonuklearen Fusion ein, bei dem Wasserstoff zu Helium fusioniert. Man spricht hier vom sogenannten „Proton-Proton-Zyklus“, bei dem zunächst zwei Protonen zu Deuterium fusionieren () und dann zwei Deuteriumkerne zu Heluim fusionieren (). Bei diesem „Wasserstoffbrennen“ stellt sich ein stabiles Gleichgewicht zwischen Strahlungsdruck und Gravitationsdruck ein. Da keine Durchmischung der zentralen Kernregion, in der das Wasserstoffbrennen zunächst abläuft, mit der äußeren Zone des Sterns stattfindet, verlagert sich das Gebiet des Wasserstoffbrennens nach dem der Kern ausgebrannt ist (also nur noch aus Helium besteht) in die äußere Schale. Wenn ein massereicher Stern seinen ganzen Wasserstoffvorrat aufgebraucht hat und der Strahlungsdruck dem Gravitationsdruck nicht mehr standhalten kann, so kommt es zu einem sogenannten Gravistationskollaps. Der Stern fällt unter seiner eigenen Gravitationskraft in sich zusammen. Durch die in dem Prozess der Kontraktion freiwerdenden Gravitationsenergie erhöht sich die Temperatur im Inneren des Sterns so weit, dass der Prozess des Heliumbrennens einsetzen kann (Vgl. Proton-Proton-Zyklus II). Hierbei bläht sich der Stern gewaltig auf, was gemeinhin als „Roter Riese“ bezeichnet wird. Ist der der Prozess des Heliumbrennens abgeschlossen, so wiederholt sich aufgrund der gleichen Ausgangslage von Strahlungsdruck und Gravitationsdruck der Gravitationskollaps, wobei sich die Zentraltemperatur weiter erhöht, sodass die Fusionsprodukte des Heliumbrennens selbst Fusionsprozesse eingehen können.

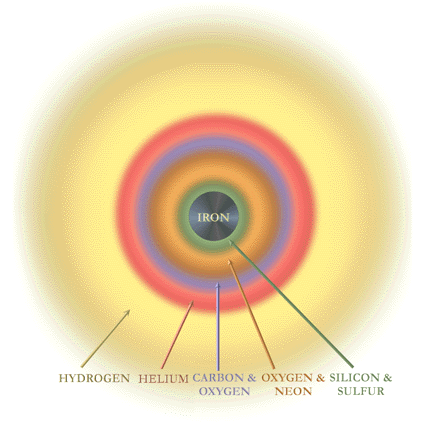
Abbildung 43 Die "Zwiebelschalenstruktur" eines sterbenden Sterns

Diese können maximal bis zu „Eisengruppe“, als Fe, Co, Ni führen, da für höhere Kernladungszahlen die Fusion endotherm abläuft, weshalb ohne Hinzuführung von Energie keine schwereren Elemente synthetisiert werden. Da die Fusion, und somit die Elementsynthese jeweils im Inneren des Sternes geschieht, kommt es zur Ausbildung der „Zwiebelschalenstruktur“ in sterbenden Sternen, wobei die einzelnen Elemente in konzentrischen Schalen angeordnet sind.Die zuletzt synthetisierten, also die schwersten Elemente befinden sich hierbei im Inneren, das leichteste, der Wassserstoff in der äußersten Schale.

Abbildung 44 Die Endentwicklung von Sternen

Je nachdem welche Masse der Stern besitzt, steht ihm ein anderes Schicksal bevor. Sterne mit einer Masse enden als sogenannte Weiße Zwerge und brennen aus, wobei der Radius um so kleiner ist, je größer die Restmasse nach Abwurf der Hülle ist. Sie sind vermutlich stabil und haben eine moderate Dichte von 1t/cm³.

Gilt für die Masse des Sterns : so kommt es zu einer sogenannten Supernovaexlosion. Dabei wird die äußere Hülle explosionsartig abgestoßen und es bildet sich ein Neutronenstern. Hierbei treten Materiedichten von bis zu g/cm³ bei Radien von ~ 10km auf..
Bei noch höheren Sternmassen ist der Gravitationskollaps nicht einmal mehr durch den Druck der Neutronen aufzuhalten und es bildet sich ein Schwarzes Loch mit unendlicher Dichte.

Die abgestoßene Hülle der Supernova stellt eine Schockfront gegenüber dem sie umgebenden interstellaren Medium dar. An dieser können Teilchen nach dem Fermimechanismus erster Ordnung beschleunigt werden. Somit sind die Gebiete fürherer Supernovaexplosionen, die sogenannten „Supernova Remnants“ (=Reste) eine potentielle Quelle für hochenergetische Teilchen.

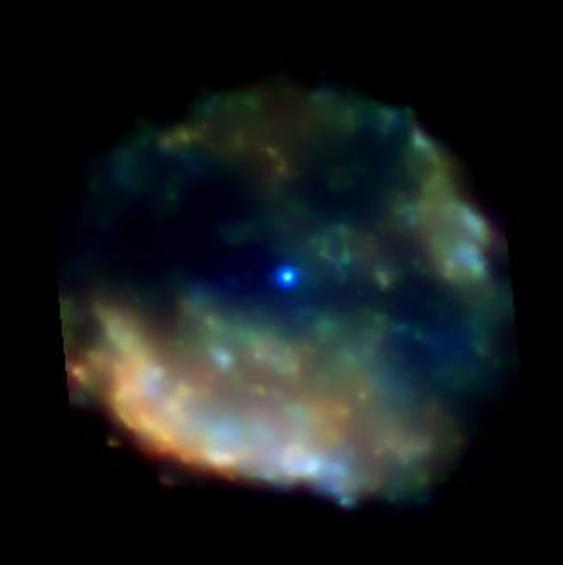
Abbildung 45 Supernovaüberrest RCW 103

Die endliche Lebensdauer einer Supernovaschockfront bewirkt auch eine Maximalenergie, bis zu der Partikel durch diesen Mechanismus beschleunigt werden können. Durch aufwändige Berechnungen mit Näherungswerten der durch die Supernovaumgebung gegebenen charakteristischen Größen erhält man eine Maximalenergie für die Beschleunigung kosmischer Strahlung durch Supernovaschockwellen.

6.2 Pulsare

Die oben erwähnten Neutronensterne offenbaren sich als noch viel interessantere physikalische Phänomäne als zunächst angenommen. Da der Drehimpuls der Sterne auch bei der Kontraktion erhalten bleibt, verkleinert sich die Umlaufzeit erheblich. Daher ergibt sich für einen Stern mit dem Radius , einem Radius des nach der Kontraktion entsandenen Neutronensterns von und einer angenommenen Umlaufzeit T von einem Monat (=2592000s) als Umlaufzeit für den entsandenen Neutronenstern :

Vereinfacht kann die Form des Sterns als Kugel betrachtet werden, deren Trägheitsmoment gegeben ist durch : . Daher ergibt sich :

.
Und analog für die Umlaufzeiten T = 1/ω :

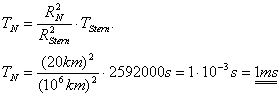
Neutronensterne sind also extrem schnell rotierende Objekte. Nun bleib auch der magnetische Fluss erhalten, weshalb sich die magnetische Flussdichte in einem Flächenstück durch die sich drastisch verkleinernde Oberfläche massiv erhöht.

Betrachtet man eine Hemisphäre, die annähernd eine Halbkugel darstellt, so ergibt sich mit einer Oberfläche A=2πr² :

Hierbei kommt es also wie man leicht sieht zu einer außerodentlichen Vergrößerung der Intensität des magnetischen Feldes.(Im oben genannten Beispiel eine Vergrößerung um den Faktor !) Analog dazu prägt sich ein ebenfalls sehr starkes elektrisches Feld aus.

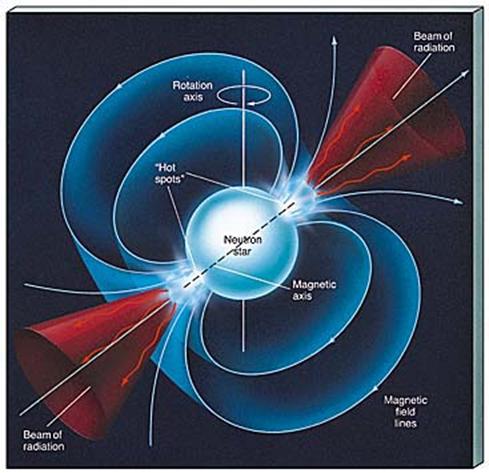
Abbildung 46 Modelldarstellung eines Pulsar

Über den magnetischen Polen wird Strahlung vom Radio- bis zum Gammastrahlenbereich in sogenannten Jets emmitiert. Aufgrund der schnellen Rotation kann es sein, dass diese Jets in regelmäßigen Abständen unser Sichtsfeld überstreichen, was zu einem „gepulsten“ Signal führt. Erstmals wurde ein gepulstes Radiosignal 1967 auf einen „Pulsar zurückgeführt.

Abbildung 47 Das orginale Radiosignal von PSR 1919+21 (1967)

Man nimmt an, dass es den Pulsaren mittels einem bisher unbekannten Mechanismus aufgrund von unipolarer Induktion in der Magnetospäre des Neutronensterns gelingt einen Teil ihrer gigantischen Rotationsenergie in kinetische Energie der Teilchen umzuwandeln und diese somit auf ultrarelativistische Energieen zu beschleunigen, wobei unweigerlich hochenergetische Photonen (γ-Quanten) emittiert werden.

Abbildung 48 Der Krebsnebel ist der Überrest der Supernovaexplosion im Jahre 1054. Im Zentrum sitzt ein Pulsar mit einer Rotationsgeschwindigkeit von 30/s.

Der vom Pulsar emittierte Plasmawind stellt wiederum eine Schockfront gegenüber dem interstellaren Medium dar, was zu den bereits diskutierten Effekten führt.

Auf die einzelne gammastrahlenerzeugende Strahlungsprozesse im Kapitel 7.1 näher eingegangen

6.3 Binärsternsysteme

Abbildung 49 Binärsternsystem mit Akkretionsscheibe

Ein Pulsar oder Neutronenstern, der einen „normalen“ Stern als Begleiter hat, zieht aufgrund seiner großen Massendichte und der daraus resultierdenden Gravitationskraft kontinuierlich Materie vom normalen Stern ab, die er in einer sogenannten Akkretionsscheibe um sich selbst sammelt. Bei diesen Prozess werden gewaltige Mengen Gravitationsenergie umgesetzt, die zu hochenergetischer Strahlung führt.Da der masseaufnehmende Neutronenstern Röntgenstrahlen emittiert spricht man hier auch von Röntgenbinären, die in Einzelfällen auch mit kleinen schwarzen Löchern anstatt der Pulsare entstehen können. Das magnetische Feld des Neutronensterns, das annähernd senkrecht auf der Akkretionsscheibe steht, muss durch eine sehr starke elektrische Kraft übernommen werden, wenn das System in ein System mit transformiert wird. Aus

ergibt sich die Teilchenenergie

Bei plausiblen Annahmen : () erhält man Teilchenenergien von eV, die Beschleunigungsmechanismen sind jedoch völlig unklar. Dies ist also nur eine prinzipielle Obergrenze.

6.4 aktive galaktische Kerne (AGN)

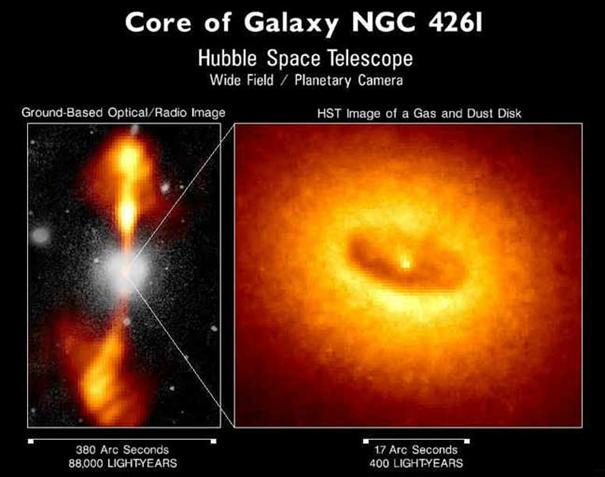
Abbildung 50 Aktive Galaxie NGC 4261

Aktive galaktische Kerne sind Galaxien von denen bipolare Jets ausgehen, die von einer Akkretionsscheibe um ein supermassives schwarzes Loch im Zentrum der Galaxie hervorgerufen werden. Man vermutet die Beschleunigung der Partikel in kleinen Regionen der relativistischen Jets. In diesen finden sich wieder Schockfronten im Plasma die ebenfalls für eine Beschleunigung verantwortlich sein könnten. Betrachtet man die Formel für die Teilchenenergie der durch Röntgenbinäre beschleunigte Teilchen, so wird klar, dass in den Akkretionsscheiben der aktive galaktischen Kerne die höchsten Energien erreicht werden.

Abbildung 51 Beschleunigungs- und Produktionsprozesse an Schwarzen Löchern

7. Gammastrahlen- und Neutrinoexperimente zur „Beweisaufnahme“

Doch wie kann man nun all diese theoretisch vermuteten Beschleunigungsmechanismen überprüfen ? Die vermuteten Beschleunigungsorte müssten Quellen von geladener kosmischer Strahlung sein, doch diese ist durch intergalaktische Magnetfelder völlig isotrop verteilt wenn es die Erde erreicht. Glücklicherweise emittieren die hochenergetischen Teilchen in verschiedenen Prozessen uneladene Teilchen, vor allem Neutrinos und Photonen, welche direkt zur Quelle „zeigen“. Jeder Strahlungsprozess erzeugt ein charackteristisches Energieflussspektrum, weshalb durch Messungen der Emissionen Rückschlüsse auf die Präsenz von hochenergetischen geladenen Teilchen an der Quelle geschlossen werden kann. Da die geladene kosmische Strahlung im unteren Spektralbereich bis zum „Knie“ bei eV durch Protonen dominiert ist, müsste man also bei den für diesen Energiebereich vermuteten Quellen, den Supernoveresten, Hinweise auf Protonenpopulationen finden, um die Beschleunigungstheorie zu bestätigen. Besonders interessant sind hierbei hochenergetische Teilchen, also Gammastrahlen und Neutrinos.

Da jedoch bis zum heutigen Tage noch kein extragalaktisches Neutrino zweifelsfrei gemessen wurde, sondern allenfalls Messungen von solaren Neutrinos geglückt sind, kann man über diese Teilchen in absehbarer Zeit noch keine Bestätigung der Beschleunigungstheorien erwarten. Doch selbstverständlich sind auch durch die Messung von atmosphärischen und solaren Neutrinos bereits sehr interessante Erkenntnissse für die Teilchenphysik gewonnen worden. So konnte das nicht mit der Erwartungen übereinstimmende Neutrinofluss über ein durch Osziallation zwischen den einzelnen Neutrinoflavours über das Flussverhältnis von Elektronenneutrinos und Myonneutrinos erklärt werden.

Grundlegende Annahme ist, dass hochenergetische Protonen in der Quelle oder auf ihrem Weg mit Kernen zusammenstoßen und somit Pionen erzeugen, ähnlich wie dies auch in der Atmosphäre geschieht.

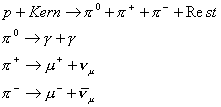
Kann man nun entweder die Gammastrahlung, oder diese Neutrinos nachweisen, wäre eine hochenergetische Protonenpopulation in der Quelle, und somit auch die Quelle als Ort der Beschleunigung belegt.

7.1 Produktionsprozesse für Gammastrahlen

Wesentlich weiter gediehen als die Neutrino-Astronomie ist die Gamma-Astronomie. Neben dem eben erwähnten Zerfall von neutralen Pionen, kommen noch weitere Produktionsprozesse für hochenergetische Gammastrahlung bei den Quellen der kosmischen Strahlung in Betracht:

Abbildung 52 Schematische Darstellung der Aussendung von Synchrotronstrahlung

Synchrotronstrahlung von Elektronen ensteht bei der beschleunigten Bewegung von Elektronen in Magnetfeldern. Für die von einem Elektron der Energie E in einem Magnetfeld mit der magnetischen Feldstärke B abgegebene Leistung P gilt :

, somit ist .

Wenn ein geladenes Teilchen durch ein Coulombfeld eines geladenen Teilchens (Atomkern oder Elektron) abgelenkt wird, emittiert dieses Bremsstrahlung. Dieser Vorgang ist grundlegend mit dem der Synchrotronstrahlung verwand, nur das hier kein Magnetfeld, sondern ein Coulombfeld einer Ladung den Ort der Abbremsung darstellt.

Abbildung 53 Der Inverse Comptoneffekt

Der Inverse Compton-Effekt ist quasi die Umkehrung des historischen Compton-Effektes, bei dem ein energiereiches Photon mit einem ruhenden Elektron zusammenstößt und dadurch Energie an das Elektron verliert, also gestreut wird. In der Astrophysik betrachtet man hochenergetische Elektronen die mit den Schwarzkörperphotonen der kosmischen Hintergrundstrahlung oder Sternenlichtphotonen zusammenstoßen und dadurch selbst Energie verlieren, während das Photon in den Gammastrahlenbereich „blauverschoben“ wird.

Genauso wie im Paarbildungsprozess aus Photonen Materie/Antimaterie Teilchenpaare gebildet werden, werden bei der Anihilierung von Teilchen und Antiteilchen Photonen gebildet. Als Hauptquelle hierfür kommt die Vernichtung von Elektron-Positronpaaren sowie in seltenen Fällen die Anihilation von Proton und Antiproton in Frage.

Aufgrund der festen Masse der Elementarteilchen, haben die entstehenden Photonen jeweils eine diskrete Energie von 511 keV, der Ruhemasse des Elektrons. Die Anihilierung von Protonen und Antiprotonen kann zum Beispiel zur Bildung von einem Pionentrio führt, das dann wie oben bereits dargestellt unter anderem in Gammaquanten zerfällt. Diese sind dann jedoch nicht mehr monoenergetisch und gibt es praktisch nicht.

Um den Nachweis für Hadronen in bestimmten Punkquellen von Gammastrahlung zu erbringen, muss man also einzelne Spektralbereiche den Prozessen zuordnen.

7.2 Ein möglicher Beweis für Supernovaüberreste als Beschleuniger für Protonen ?

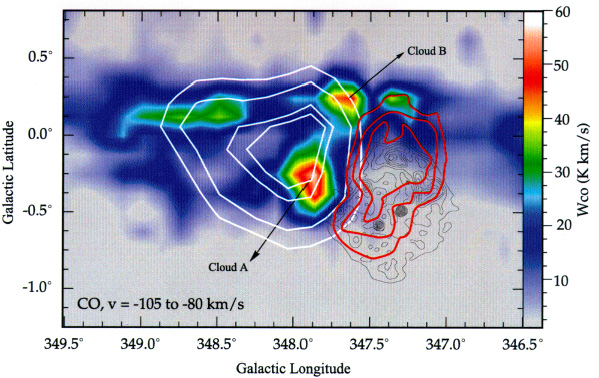
Abbildung 54 Eine Überblendungskarte von SNR RX J1713.7-3946 in galaktischen Koordinaten, wobei die roten Linien die TeV Daten von CANGAROO wiedergeben, die wei0en Linien die wahrscheinliche Guelle der GeV Messung durch EGRET darstellen und die grauen Linien die gemessenen Röntgenstrahlen symbolisieren.

Im Jahre 2002 veröffentlichten Wissenschaftler die am CANGAROO-Projekt, einem Luftčerenkovteleskop zur Beobachtung kosmischer Gammastrahlung, einen Möglichen Hinweis auf Hadronen im Supernovarest RX J1713.7-3946 [R 9]. Hierzu wurden Daten vom CANGAROO-Teleskop sowie dem Satellitenexperiment EGRET im Rahmen des Compton Gamma Ray Observatory, dem Australia Telescope Compact Array (ATCA) und ASCA im Satelliten ROSAT von dieser Quelle in einem Fluss-Energie-Diagramm aufgetragen.(Abbildung 55)

Nun wurde versucht die Prozesse Synchrotron-/Bremsstrahlung, Inverser-Compton-Effekt und Zerfall neutraler Pionen mit gewählten Magnetfeldstärken in dieses Diagramm einzupassen. Bei einem gewählten Magnetfeld von 4.06–0.58 μG ergab sich die als durchgezogene Linie gezeichnete Kurve, welche mit den Messdaten in Übereinstimmung steht.

Für den Prozess des inversen-Compton-Effektes wurden die 2,7 K Photonen der kosmischen Hintergrundstrahlung als Stoßpartner angenommen. Die für zwei repräsentative Magnetfeldstärken von 3 μG und 10 μG gezeichneten Kurven (kurz gestrichelte Linien) zeigen deutlich, dass der durch diesen Prozess entstehende Kurvenverlauf für kein B bei den zur Berechnungen der Synchrotronstrahlung angenommenen Eigenschaften der Quelle mit den Messdaten in Übereinstimmung zu bringen ist.

Nachdem auch mit erhöhtem Aufwand und unter Verwendung von diversen Modellen keine Übereinstimmung abzusehen war, überprüften die Wissenschaftler das bei einem -Zerfall entstehende Spektrum. Unter gleichen Bedingungen ergibt sich hier ein Kurvenverlauf, welcher durchaus mit den Messdaten in Einklang zu bringen ist. Somit ist hier (eventuell)der Nachweis erbracht worden, das Supernovaüberreste Protonen auf Energien von mindestens einigen TeV beschleunigen können.

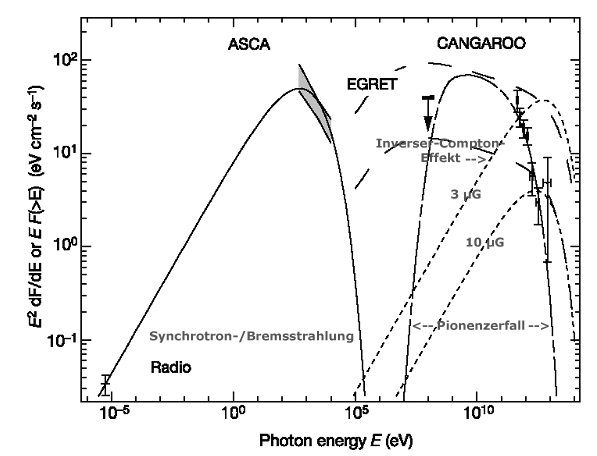
Abbildung 55 Multibandemmisionen von RX J1713.7-3946

Doch leider bereitet die Obergrenze von EGRET hier einige Probleme, weshalb weitere Beobachtungen von Gammastrahlen im TeV-Bereich nötig sind um zuverlässigere Aussagen treffen zu können.

7.3 Das H.E.S.S. Projekt

Das „High Energy Stereoscopic System“ ist ein stereoskopisches System von Telekopen zur Aufzeichnung der durch (kosmische) Gammaquanten im TeV-Bereich in der Atmosphäre hervorgerufenen Luftčerenkovstrahlen. Es entsteht derzeit im Khomas-Hochland in Namibia auf dem afrikanischen Kontinent, etwa 100km südwestlich der Hauptstadt Windhoek. Die genau geographische Lage ist 23°16’18“ S, 16°30’00“ E, bei 1800 m über NN.

Abbildung 56 Das nunmehr komplette H.E.S.S. in Namibia

Seit Dezember 2003 sind alle 4 in der ersten Phase des HESS-Projektes geplanten Teleskope installiert und nehmen Daten auf. Ein Teleskop besteht aus 382 individuellen Spiegeln, die auf einer hexagonalen Schüssel mit einem Durchmesser von 12 m montiert sind. Jeder Spiegel kann durch hochpräzise Motoren mit einer Genauigkeit von einigen Tausendstel Millimetern genau ausgerichtet werden. Das Herzstück eines Teleskop ist die Kamera, welche bei einem Focus von 15m angebracht ist. Eine Kamera besteht aus 60 Segmenten mit jeweils 16 Photomultipliern, hat einen Durchmesser von 1,5m und ein Gewicht von 820 kg. Besondere Eigenschaft dieser Kamera ist die äußerst kurze „Verschlusszeit“ (~10 ns), die ein genaues Beobachten ohne den „visuellen Hinterundlärm“ erst ermöglicht, da es sich wie bei den Erläuterungen zum Čerenkoveffekt bereits erwähnt, hier um sehr kurze „Lichtblitze“ handelt. Es handelt sich hierbei um eine elektronische Kamera, die das Licht über eine Zeit von etwa 10 ns integriert und davon sogenannte „Trigger“ ableitet.

Abbildung 57 Eine der Kameras der HESS Teleskope

Besonderheit der steroskopischen Beobachtung ist nun, dass die Teleskope über eine spezielle Triggerhardware synchron ausgelöst werden. Mit den in einem Quadrat von 120m² postierten Teleskopen kann man so beim Betrachten der Quelle unter verschiedenen Winkeln die Richtung des Gammateilchens genau rekonstruieren. Aus der Intensität des Abbildes lassen sich Rückschlüsse auf die Primärenergie des Teilchens ziehen, während die Form Auskunft über die Art des Primärteilchens gibt. Besonderes Augenmerk gilt hier also der sogenannten „Schauerrekonstruktion“, jener durch den Rechner übernommene Aufgabe bei der aus den Messdaten Aussagen über das Primärteilchen errechnet werden.

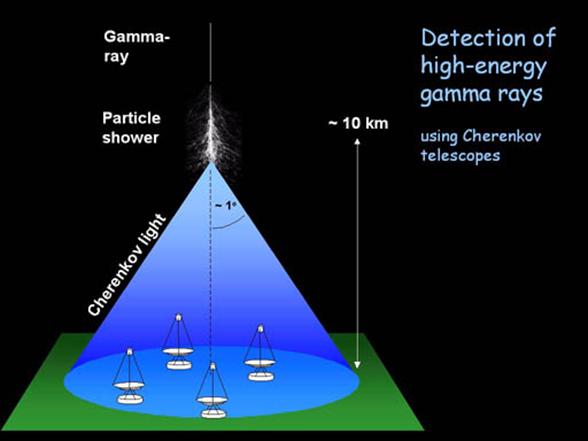
Abbildung 58 Das Prinzip der Detektion von Gammastrahlen mit stereoskopischen Ĉerenkovteleskopen

Abbildung 59 Erstes durch alle 4 Teleskope gemessenes Ereignis vom 10. Dezember 2003

Nachdem in der Nacht des 10. Dezember 2003 die ersten Koinzidenzmessungen mit allen 4 Teleskopen gelangen, erhofft man sich interessante und aufschlussreiche Daten um das nunmehr 100 Jahre Alte Rätsel der Quellen der kosmischen Strahlung (weiter) lüften zu können oder gar neue zu entdecken. Eine interessante Entdeckung sind hier auch die sogenannten Gamma-Ray-Bursts, welche absolute Priorität bei der Beobachtung haben. Das heißt, das jegliche Beobachtung unterbrochen wird, sobald ein Gamma-Ray-Burst registriert wurde und stattdessen in Richtung des Ausbruchs gemessen wird.

7.4 Exkurs: Gamma Ray Bursts

Als in den späten sechziger Jahren die atomare Aufrüstung sowie die Raumfahrt immer größere Außmaße annahm, kam es zum Start der Vela Satelliten durch die US Air Force. Diese sollten Gammastrahlen in der Atmosphäre detektieren, die von Atombombenexplosionen stammen könnten. Politische Motivation war die Überwachung der Einhaltung des Übereinkommens gegen die Durchführung oberirdischer Kernwaffentests. Nach diesem war die Detonation von Kernwaffen zu Testzwecken im Weltraum und der Atmosphäre untersagt. Eine Erklärung ist Millitärs selten Beweis genug und so kam es das die US Air Force „geheime“ Tests der UdssR auf der Rückseite des Mondes, wo eine optische Registrierung des illegalen Tests unmöglich wäre, befürchtete. Als 1967 dann tatsächlich kurze Gammastrahlen-„Blitze“ aus allen möglichen Himmelsrichtungen gemessen wurden, war die Spannung im ohnehin eskalierenden Ost-Westkonflikt auf einem neuen Höhepunkt. Die politische Lage entspannte sich jedoch wieder, als die kosmische Herkunft der Gammastrahlenblitze belegt wurde.

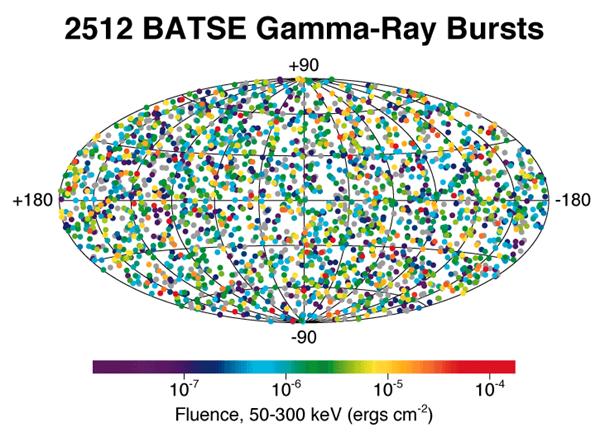
Abbildung 60 Die Verteilung der durch BATSE beobachteten GBR's

Gamma Ray Bursts treten plötzlich und in einer unvorhersehbaren Rate auf. Sie sind mit einer Lebensdauer von 30 ms bis 1000 s sehr kurze Ereignisse, dafür aber von erheblicher Intensitätsschwankung gekennzeichnet. Ziemlich schnell nach ihrer Entdeckung stellte sich herraus, dass GRB über den gesammten Himmel „zufällig“ verteilt auftreten. Dies lässt eine galaktische Herkunft als unwahrscheinlich erscheinen, da sonst eine Konzentration in der galaktischen Scheibe, wie sie zum Beispiel bei „normalen“ (also vergleichsweise dauerhaft beständigen) Gammastrahlen die mit dem EGRET Experiment von COMPTEL gemessen wurden, zu erkennen sein müsste. (Abbildung 61)

Abbildung 61 Aufnahme des Gammstrahlenhimmels durch EGRET

1997 gelang erstmals die Assoziation von einem GRB und einer optischen Quelle. Als man die Rotverschiebung im Spektrum der optischen Quelle berechnet hatte und somit auf die Entfernung des GRB schließen konnte, wurde klar, dass er quasi „vom Rande unseres Universums“ stammte, also mehrere Milliarden Lichtjahre entfernt stattfand. Inwiefern sich das für alle GRB’s gilt bleibt abzuwarten. Dies macht diese Erscheinung ungemein interessanter, da ungeheure Energiemengen freiwerden müssen, um aus so großen Entfernungen mit so großen Intensitäten zu uns zu gelangen. Man vermutet, dass sie unter anderem durch die Kollision von zwei Neutronensternen, bei der ein schwarzes Loch entsteht, bzw beim Kollabieren eines supermassiven Sterns (), bei denen ebenfalls ein schwarzes Loch entsteht, erzeugt werden. Andere Theorien vermuten das ein durch eine Supernovaexplosion entstandener Neutronenstern binnen Jahresfrist in sich zu einem schwarzen Loch kollabiert.

In letzter Zeit hat man unter anderem ein Nachleuchten im Bereich der Röntgenstrahlen und des „sichtbaren“ Lichtes beobachtet, was die Entfernungsbestimmungen über die Rotverschiebung ermöglichte. Da die GRB-Quellen trotz ihrer kosmischen Entfernung noch so „hell“ leuchten, müssen sie Energiemengen freisetzen, die alle bisher bekannten Objekte des Universums übersteigen – vergleichbar mit dem Leuchten der gesamten Milchstraße in 100 Jahren.

Abbildung 62 Künstlerische Impresion eines Gamma-Ray-Bursts

8. Zusammenfassung und Ausblick

Obwohl die Entdeckung der kosmischen Strahlung beinahe 100 Jahre zurückliegt, ist sie noch immer eines der interessantesten Phänomene der Astrophysik. Besonders die Beschleunigungsmechanismen, welche es vermögen, Teilchen auf solch hohe Energien zu bringen, sind bis heute nicht eindeutig geklärt und nicht mit experimentellen Messdaten zu beweisen. Die Anzahl der sich im Aufbau befindender oder bereits operierenden Teleskope zur Untersuchung der kosmischen Strahlung (Auger, HESS, HiRes, AMANDA, Kaskade Grande) gibt zur Hoffnung auf neue aufschlußrecihe Messdaten Anlass, anhand derer aktuell diskutierte Theorien zur Beschleunigung und Propagierung der kosmischen Strahlung gestützt oder widerlegt werden können. Als mögliche Beschleunigungsmechansimen werden zwei wesentliche Gruppen betrachtet : statistische Beschleunigungsprozesse in magnetisiertem Plasma (Fermi-Beschleunigng) und die Beschleunigung geladener Teilchen durch sehr starke elektrische Felder wie etwa bei Pulsaren.

Die Untersuchung der Quellen ist ein physikalisch besonders interessantes Unterfangen, da hier Grenzen des uns Bekannten erreicht werden, an denen Theorien, die im irdischen Bezugssytem bereits außer Frage stehen, erneut getestet werden können.

Besonders interessante Ergebnisse könnte die Ermittlung des Gammastrahlenspektrums bei sehr hohen Energiene (z.B. durch CANGAROO, HESS, VERITAS) bringen. Zum Beispiel könnten Spektrenabbrüche („Cut-Offs“) bei hohen Energien Hinweise auf intergalaktische diffuse Strahlungsfelder darstellen.

Das ultimative Ziel aller an Projekten bezüglich kosmischer Strahlung arbeitender Physiker ist es wohl bisher unbekannte Phänomene zu beobachten. So ist es denkbar, dass bisher theoretisch vorrausgesagte Teilchen, welche direkt nicht nachweisbar sind, also kosmische toplogische Defekte wie zum Beispiel kosmische Strings, Gravitonen, die Transferteilchen der gravitativen Wechselwirkung, oder diverse Kandidaten für die „dunkle Materie“, also jene Materie die durch keine Form der Strahlung sichtbar ist, aber zur Formung der kosmischen Strukturen, z.B. der Galaxien, wie wir sie sehen zwangsläufig vorhanden sein muss, irgendwelche detektierbaren Strahlungsüberreste in Form von Neutrinos, Gammastrahlen oder Ähnlichem hinterlassen, die dann mithilfe der aktuellen oder zukünftiger Experimente gemessen werden können. Somit sind Experimente zur Messung von kosmischer Strahlung interessante „Datenquellen“ sowohl für die Teilchen- und Astrophysik, als auch für die Astronomie und Kosmologie.

Abbildung 63 "Der Blick in die Vergangenheit" Aufnahme weit entfernter Galaxien durch das Hubble Space Telescope

Anhang A : Quellen

A.1 Quellen der Abbildungen

Abbildung 1 http://adc.gsfc.nasa.gov/mw... 1

Abbildung 2 http://www.auger.org/photos/PA013.300dpi.jpg.. 4

Abbildung 3 J.G.Willson & G.E. Perry, Cosmic Rays (Taylor and Francis,1976) 5

Abbildung 4 J.G.Willson & G.E. Perry, Cosmic Rays (Taylor and Francis,1976) 6

Abbildung 5 "Verbotene" und "erlaubte" Zonen für geladenen Teilchen.. 6

Abbildung 6 L.I.Mairoshnitschenko, Kosmische Strahlung im interplanetaren Raum (Akademie-Verlag, 1979) 7

Abbildung 7 Claus Grupen, Astroteilchenphysik (Vieweg, 2000) 7

Abbildung 8 http://www.exploratorium.edu/learning_studio/auroras/images/magnetosphere.jpg 8

Abbildung 9 http://www.auger.org/photos/PA014.web1.jpg.. 9

Abbildung 10 http://www.hep.man.ac.uk/babarph/babarphysics/images/positron.gif. 9

Abbildung 11 http://clubastronomie.free.fr/histoire/astro_pretre/Penzias.JPG.. 10

Abbildung 12 http://map.gsfc.nasa.gov.. 11

Abbildung 13 http://map.gsfc.nasa.gov.. 12

Abbildung 14 http://map.gsfc.nasa.gov.. 12

Abbildung 15 http://map.gsfc.nasa.gov.. 13

Abbildung 16 http://map.gsfc.nasa.gov.. 14

Abbildung 17 www.wkap.nl/prod/a/ISBN_0-7923-7196-8_29.PDF. 15

Abbildung 18 http://www.europhysicsnews.com/full/17/article2/Boratav_fig01.jpg.. 16

Abbildung 19 http://www.weizmann.ac.il/physics/heap/Group/Images/CRfig_big.gif. 18

Abbildung 20 Claus Grupen, Astroteilchenphysik (Vieweg, 2000) 19

Abbildung 21 http://itss.raytheon.com/cafe/ qadir/q2953.html. 20

Abbildung 22 M. Lemoine & G.Sigl(Eds.), Physikcs and Astrophysics of Ultra-High-Energy Cosmic Rays (Springer 2001) 21

Abbildung 23 Claus Grupen, Astroteilchenphysik (Vieweg, 2000) 23

Abbildung 24 http://www.brantacan.co.uk/Cerenkov13G.gif. 24

Abbildung 25 http://www.lns.cornell.edu/~e23wiz/RET/images/cheren2.jpg.. 25

Abbildung 26 http://www.gae.ucm.es/~emma/tesina/node4.html. 26

Abbildung 27 http://www.astroteilchenphysik.de/grafik/topics/cr/espek_steil_s.gif. 27

Abbildung 28 http://www.astroteilchenphysik.de/ 28

Abbildung 29 http://www.astroteilchenphysik.de/ 29

Abbildung 30 http://www.astroteilchenphysik.de/ 30

Abbildung 31 http://www-ik.fzk.de/KASCADE_home.html. 31

Abbildung 32 http://www.physics.adelaide.edu.au/astrophysics/HiRes.html. 31

Abbildung 33 http://www.physics.adelaide.edu.au/astrophysics/HiRes.html. 32

Abbildung 34 http://www.auger.org/ 33

Abbildung 35 http://www.auger.org/ 33

Abbildung 36 http://www.auger.DE/ 34

Abbildung 37 http://amanda.uci.edu/ 34

Abbildung 38 http://amanda.uci.edu/ 35

Abbildung 39 http://amanda.uci.edu/ 36

Abbildung 40 http://www.lucidcafe.com/library/95sep/95sepgifs/fermi.gif. 37

Abbildung 41 links : Gaisser, Thomass K., Cosmic Ray and Particle Physics (Cambridge Univ. Press 1990)
rechts : Claus Grupen, Astroteilchenphysik (Vieweg, 2000) 38

Abbildung 42 links : Gaisser, Thomass K., Cosmic Ray and Particle Physics (Cambridge Univ. Press 1990)
rechts : Claus Grupen, Astroteilchenphysik (Vieweg, 2000) 39

Abbildung 43 http://cosmos.colorado.edu/astr1120/superPre-72.giF. 42

Abbildung 44 http://www.seasky.org/cosmic/images/starlife.jpg.. 43

Abbildung 45 http://www.astro.psu.edu/xray/snr/rcw103.jpg.. 44

Abbildung 46 http://cosmos.colorado.edu/astr1120/pulsar.jpg.. 46

Abbildung 47 Lyne, A.G. & Graham-Smith, F., Pulsare (Barth 1993) 47

Abbildung 48 http://antwrp.gsfc.nasa.gov/apod/image/9911/crab_vlt.jpg.. 47

Abbildung 49 http://antwrp.gsfc.nasa.gov/apod/image/9912/accretiondisk_hst_big.gif. 48

Abbildung 50 http://www.lanl.gov/milagro/images/ngc_4261_lg.jpg.. 49

Abbildung 51 Beschleunigungs- und Produktionsprozesse an Schwarzen Löchern.. 49

http://astrosun.tn.cornell.edu/courses/astro201/images/synch_rad.gif. 50

Abbildung 53 http://venables.asu.edu/quant/proj/Inverse.gif. 51

Abbildung 54 http://www.roma2.infn.it/users/aldo/butt01.pdf. 52

Abbildung 55 Nature Vol. 416, 823, (2002), „The acceleration of cosmic-ray protons in the supernova remnant RX J1713.7-3946. 53

Abbildung 56 http://www.mpi-hd.mpg.de/hfm/HESS/HESS.html. 54

Abbildung 57 http://www.mpi-hd.mpg.de/hfm/HESS/HESS.html. 54

Abbildung 58 http://www.mpi-hd.mpg.de/hfm/HESS/HESS.html. 55

Abbildung 59 http://www.mpi-hd.mpg.de/hfm/HESS/HESS.html. 567

Abbildung 60 http://www.batse.msfc.nasa.gov/batse/grb/skymap/images/fig2_2704.pdf. 578

Abbildung 61 http://heasarc.gsfc.nasa.gov/Images/objects/heapow/large_scale_structure/egret_allsky2a.gif 59

Abbildung 62 http://chandra.harvard.edu/photo/2003/grb020813/grb020813_illustration.ps 60

Abbildung 63 http://www.udstillinger.dnlb.dk/astroweb/Images/NASA-Hubble/HDFWF3-300.gif 601

A.2 Literatur :

Asimov, Isaac, “Atom” (Trueman Talley Books, 1992)

Cox, Arthur N. (Eds.), “Allen's Astrophysical Quantities” (Springer, 2000)

Dautcourt, Georg, “Relativistische Astrophysik” (Akademie-Verlag, 1976)

Gaisser, Thomass K., Cosmic Ray and Particle Physics (Cambridge Univ. Press 1990)

Grupen, Claus, „Astroteilchenphysik“ (Vieweg, 2000)

Harwin, Martin , „Astrophysical Concepts“ (Springer, 1998)

Hawking, Stephen, „The Universe in a Nutshell“ (Random House 2001)

Kleinknecht, K, „Detektoren für Teilchenstrahlung“, (Teubner 1992)

Lemoine, M. & Sigl, G.(Eds.), “Physikcs and Astrophysics of Ultra-High-Energy Cosmic Rays” (Springer 2001)

Lyne, A.G. & Graham-Smith, F., “Pulsare” (Barth 1993)

Mairoshnitschenko , L.I., “Kosmische Strahlung im interplanetaren Raum” (Akademie-Verlag, 1979)

Prölss, Gerd W, “Physik des erdnahen Weltraums” (Springer 2001)

Schäfer, Hans, “Elektromagnetische Strahlung” (Vieweg 1985)

Sharpio, Maurice M. & Wefel, John P.(Eds.), “Cosmic Gamma Rays, Neutrinos, and Related Astrophysics” (Kluwer 1988)

Treichel, Michael, „Teilchenphysik und Kosmologie“, (Springer 2000)

Wilson, J.G. & Perry, G.E., „Cosmic Rays“ (Taylor and Francis,1976

Metzler Physik

Tipler Physik

A.3 Internetquellen :

http://www.mpi-hd.mpg.de/hfm/HESS/HESS.html

http://amanda.uci.edu/

http://www-ik.fzk.de/KASCADE_home.html

http://www.astroteilchenphysik.de/

http://www.physics.adelaide.edu.au/astrophysics/HiRes.html

http://www.auger.org/

http://map.gsfc.nasa.gov/

http://aether.lbl.gov/www/projects/cobe/

http://en2.wikipedia.org/wiki/Cherenkov_effect

http://besch2.physik.uni-siegen.de/~depac/DePAC/DePAC_tutorial_database/grupen_istanbul/node12.html

http://www.ps.uci.edu/~silvestri/thesis/THESIS/node38.html

http://www.gae.ucm.es/~emma/tesina/node4.html

http://www.cosmic-ray.org/

http://pdg.lbl.gov/2000/cosmicrayrpp.pdf

www.wkap.nl/prod/a/ISBN_0-7923-7196-8_29.PDF

A.4 Zeitschriften & Conference Publications

Nature Vol. 416, 823, (2002), „The acceleration of cosmic-ray protons in the supernova remnant RX J1713.7-3946

Physical Review, Vol 75, Nr. 8, S. 1169, (1949), “On the Origin of the Cosmic Radiation”, Enrico Fermi

The 28^th Cosmic Ray Conference, “Serach for Extremely High Energy Gamma Rays with the KASCADE Experiment”

The 28^th Cosmic Ray Conference, “The KASCADE experiment”

Anhang B Glossar

CANGAROO	Luftcherenkoteleskop zur Messung kosmischer Gammastrahlen in Australien
CBR	Kosmische Hintrgrundstrahlung (Cosmic Background Radiation)
COBE	Cosmic Background Explorer – Satellit der NASA zur Messung der kosmischen Hintergrundstrahlung
CR	Kosmische Strahlung
EAS	Großflächiger Teilchenschauer in der Atmosphäre (Extensive Airshower)
EHE CR	Kosmische Strahlen der höchsten Energien (Extreme High Energy Cosmic Rays)
GBR	Gamma-Ray-Burst
HESS	High Energy Stereoscopic System, Gammastrahlenteleskop in Namibia
SNR	Super Nova Remnant, der Überrest einer Supernovaexplosion
VERITAS	Luftcherenkovteleskop zur Messung kosmischer Gammastrahlung in den USA
WMAP	Wilkinson Microwave Anisotropy Probe = Satellitenexperiment der NASA zur genauen Vermessung der kosmischen Hintergrundstrahlung

Anhang C Ausgewählte Referenzen

R 1 V.F.Hess: Phys. Z. 13, 1084 (1912)

R 2 W. Kohlhörster: Phys. Z. 14, 1153 (1913)

R 3 Penzias, A. A.; Wilson, R. W Astrophys. J, 142, 419. (1965)

R 4 K. Greisen: Phys. Rev. Lett. 16, 748 (1966)

G. T. Zatsepin, V.A. Kuzmin, Pis’ma Zh. Eksp. Teor. Fiz. 4, 114 (1966)

R 5 R T.K. Gaisser, A.M. Hillas: proc. 15th Int. Cosmic Ray Conf. (plovdiv), 8, 353 (1977)

R 6 P.A. Cherenkov, Phys. Rev., 52, 378 (1937)

R 7 R. Bunner, Cosmic Ray Detecion by Atmospheric Fluorescence, Ph.D. Thesis, Cornell University

R 8 E. Fermi: Phys. Rev. 2^nd ser., 75, no 8, 1169 (1949)

R 9 R. Enomoto et. al., Nature 416, 823 (2002)

[1] (Es versteht sich bei der Komplexität der Materie von selbst, dass der Beschleunigungsmechanismus in turbulenten Plasmen hier nur anhand von stark vereinfachten Modellbetrachtungen angedeutet werden konnte. Insbesondere wurde angenommen, dass die Testpartikel bereits hinreichend relativistisch sind, so dass gilt.)