Looking Beyond the relaxation time approximation
Table of Contents
1. Overall scheme of electron scattering in metals
- Electrons in the metals are scattered mainly due to two mechanisms:
- Scattering from the impurities present in the lattice or the vacant sites in the lattice.
- Scattering due to non-ideal periodicity due to thermal vibration of the ions.
- At high temperature scattering due to thermal motion of the ions is important, however, at low temperature scattering due to impurities are important.
- Scattering due to electron electron process is negligible, apart from very clean samples and at very low temperatures.
2. Scattering probability of electrons
- For the case of beyond relaxation time approximation ("remember in relaxation time approximation we assume that the relaxation time is a given function momentum \(\mathbf{k}\), i.e \(\tau(\mathbf{k})\)"), one finds that the relaxation time depends not only on \(\mathbf{k}\) but also on the electron distribution function \(g(\mathbf{k})\) through the equations:
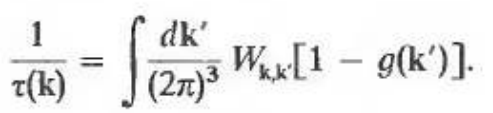 Here \(W_{k,k'}\) represent the probability of electrons scattering from the $k$-th state to the $k'$-th state.
Here \(W_{k,k'}\) represent the probability of electrons scattering from the $k$-th state to the $k'$-th state. - From above equation, the next step is to find the electron distribution function \(g(k)\). It is found by dynamic variable velocity of the (\(\frac{d g(k)}{dt}\)), which is summation of the velocity of incoming (\(\frac{d g(k)}{dt}|_{\text{in}}\)) and outgoing (\(\frac{d g(k)}{dt}|_{\text{out}}\)) electronic distribution function.
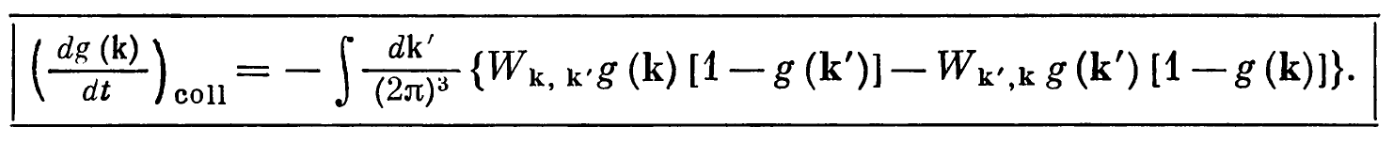 A comparison with the relaxation time approximations:
A comparison with the relaxation time approximations:

- After getting (\(\frac{d g(k)}{dt}\)) we need to connect to the real materials parameters. This is done through Boltzmann equations.
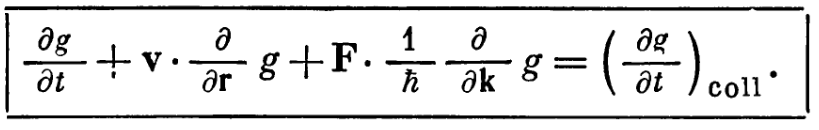
3. Is this method better than relaxation time method?
- To understand the effectiveness of the procedure going beyond the relaxation time we should compare the results from this method with the results found from the usual relaxation time approximations.
3.1. Wiedmann-Franz law
- The first such effect is the Wiedmann-Franz law. It is applicable only when the energy is saved during the scattering of electrons. The Wiedmann-Franz law is the ratio between the electronic charge current and heat current. The electronic charge current can decrease when the velocity changes. However change in velocity will also result in change in heat currents as shown in following equations:
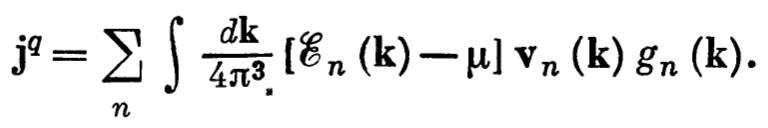 However in the above equations heat current is also proportional to the energy \(\mathcal{E}_{n}(k)\). The change in heat current will be proportional to the change in velocity of electron only if the energy of the initial and final states will be same: \(\mathcal{E}_{n}(k)=\mathcal{E}_{n}(k')\), in other words in case of elastic collisions. For the inelastic collision the energy will also change, hence there will be effect of change in velocity and change in energy.
However in the above equations heat current is also proportional to the energy \(\mathcal{E}_{n}(k)\). The change in heat current will be proportional to the change in velocity of electron only if the energy of the initial and final states will be same: \(\mathcal{E}_{n}(k)=\mathcal{E}_{n}(k')\), in other words in case of elastic collisions. For the inelastic collision the energy will also change, hence there will be effect of change in velocity and change in energy. - Usually the Wiedmann-Franz law is applicable only for low or high temperature, because only at these temperatures the condition for the elastic collision is satisfied. At low temperature the scattering is only due to impurities, for which loss in energy is small compared to \(k_{B}T\). At high temperature the scattering is mainly due to the crystal vibration (phonon), for which also the change in energy is small compared to \(k_{B}T\).
3.2. Matthiessen's Rule
- Mathiessens rule is applicable only for the relaxation time approximation, i.e. relaxation time is independent of momentum and momentum distribution function. It can only be used as the lowest possible resistivity.