Semi-Classical Theory of Conduction in Metals

1. Relaxation time approximation
2. Non-equilibrium distribution function
3. Simplification of the distribution functions
4. Application of distribution function
5. Distribution function when $H \neq 0$

1. Relaxation time approximation

In this approximation we first define two types of distribution: (i) the non-equilibrium distribution, (ii) the equilibrium distribution. It is represented as $g_{n}(r,k,t)$; it depends on band number $n$, space $r$, wave number $k$ and time $t$. In equilibrium the non-equilibrium distribution function has the same form as the fermi distribution. Hence equilibrium distribution is same as the Fermi distribution. The non-equilibrium condition appears when external field is applied, otherwise equilibrium distribution function is used.
The relaxation time $\tau_{n}(k,r)$ now depends on the band number $n$, wave number $k$ and position $r$. In the free electron approximation this was absent.
The two major approximations in the relaxation time treatment of the problem:
1. During collision electrons completely lose the information of the non-equilibrium distribution functions they possessed just before collision, and after collision the new non-equilibrium distribution will be the same as the position of the collision.
2. The electron collision can not change the distribution function.
In relaxation time approximation we define the quantity $dg_{n}(r,k,dt)$ which describes the distribution of the electrons in band $n$, at position $r$, wave number $k$ and time $dt$ after collision. From assumption 1, we understand that at each collision electrons forget their previous distribution function. Hence, if we find a single $g_{n}(r,k,t)$ it will be applicable to all the electrons (different $n,r,k,t$). The easiest distribution is the Fermi distriubution. The second assumptions says that the collision can not change this distribution with change in $n,r,k,t$. Hence, the first assumption says that if we have single distribution it is applicable to all the electrons, and second assumption says that the form of this distibution does not change with change in the $n,r,k,t$.
During collision the electrons go from one $n,r,k$ to another $n,r,k$, however the second assumption tells us that the form of the distribution should not change with collision. Hence, if the number of electrons do not change in the given $n,r,k$ other electrons should fill the emptied states. This is the relaxation time approximation.
In short, the first approximation decides the form of the distribution which can be applied to all the electrons, and second approximation says that as the distribution function does not change with collision, hence, after collision if some state is emptied, other electrons should fill these states. Mathematically:

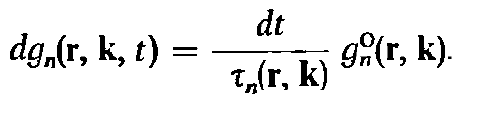
2. Non-equilibrium distribution function

The non equilibrium distribution function is derived as:
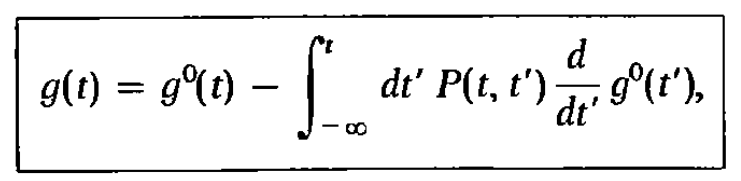
Here in deriving this we assumed that all the symbols contains the number of the zone $n$, spatial coordinate $r$, momentum $k$. As the above equation is same for all $n,k,r$ we have removed these extra indexes. Following are the meaning of the terms:
- $g(t)$ is the non-equilibrium distribution function at time $t$
- $g^{0}(t)$ is the equilibrium distribution function at time $t$
- $P(t,t')$ is the probability of the electrons survive upto time $t$, if the collision was occurred at $t'$
The integration is take over the dummy time variable $t'$. The equilibrium functions $g(t)$, and $g^{0}(t)$ depends on the time through the variable $r(t)$ and $k(t)$.
The integral term can be written as \[\int\limits_{-\infty}^{t}dt' P(t,t') \frac{d}{dt'} g^{0}(t') = \sum\limits_{-\infty}^{t} P(t,t') dg^{0}(t').\]
From above equation the meaning of the integral terms is the summation of the change in the equilibrium distribution function at every time $t'$ multiplied by the probability $P(t,t')$.
The change in the distribution function at any time $t'$ is the same as the electron experiencing the collision. Hence multiplying these freshly collided electrons with the probability of their surviving upto time $t$ we will get the extra number of the electrons occurring at time $t$ due to collision at time $t'$. These extra electrons occurring at time $t$ is the deviation from the equilibrium distribution function.
In other words, the non-equilibrium distribution function at time $t$ is found by subtracting from the equilibrium distribution function at time $g^{0}(t)$ the deviation due to collsion at time $t'$, i.e. $P(t,t')dg^{0}(t')$.
The $g^{0}(t)$ is assumed as Fermi distribution, hence we assume that it is known. $P(t,t')=1- \frac{t-t'}{\tau(t')}$ is also assumed to be known.
The differentiation of the $g^{0}(t')$ is found as: 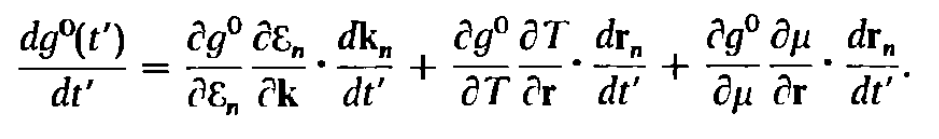As the equilibrium distribution function contains terms $\varepsilon_{n}(k(t))$, $T(r(t))$, $\mu(r(t))$ we have such complicated differentiation. Moreover if the temperature dependent directly on the time, i.e. $T(r(t),t)$ then we should have added the terms $\frac{dT}{dt}$ to above equation. The same is true for the chemical potential $\mu(t)$; in this case we should have added the term $\frac{d \mu}{dt}$ to the above equation.
One can use the semi-classical equations

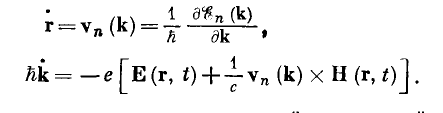
to represent the non-equilibrium distribution function:

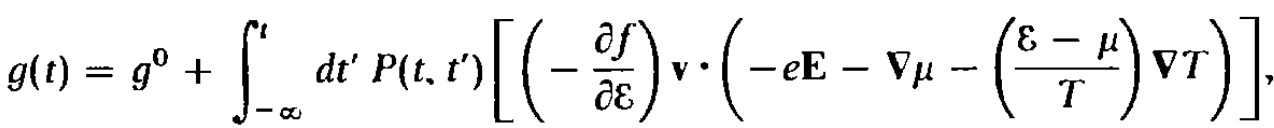
3. Simplification of the distribution functions

We consider three cases of the simplification:
1. Zero electric field and constant temperature
2. Isotropic electric field, temperature gradient and relaxation time
3. Relaxation time dependence on energy
Before further discussion we should remember in the relaxation time approximation we assumed that relaxation time is a function of the band $n$, wave vector $k$, position $r$, and time $t$.
Case 1:
- The electric field part of the non-equilibrium distribution function is: \[\int\limits_{-\infty}^{t} dt' P(t,t') \left(-\frac{\partial f}{\partial \varepsilon}\right) \frac{\partial \varepsilon}{\partial k} \left( -e E \right).\]
- The value of $P(t,t')$ is non zero only for $t'<\tau$, hence, the integration has non-zero values for a very small time frame. In means the electric field which changes the momentum $k$ according to relation $k(t)=k(0)+eEt'$ changes very little, as $\tau$ is very small.
- If the $k(t)$ changes little then $\partial f/\partial \varepsilon(k)$ also changes very little. Besides the velocity $v=\partial \varepsilon/\partial k$ also changes very little. It means we can complete neglect the terms containing the electric field. It is the same as putting the electric field to zero.
- Regarding temperature gradient, as mentioned above the integration is non-zero only for $t'< \tau$, the spatial gradient of the temperature $\nabla T$ for $\tau$ is equal to the change in the temperature during single electron free path, which is very small. In this case $\nabla T/T \approx 0$. Hence we can neglect the terms containing the temperature also.
- In further simplification the change in chemical potential can also be neglected as the chemical potential depends on the temperature.
- Hence we are left with the equilibrium distribution function with a small correction: \[g(t) = g^{0}+\delta g (t).\]
Case 2:
- To understand it we should look at the initial equation of the non-equilibrium distribution function:
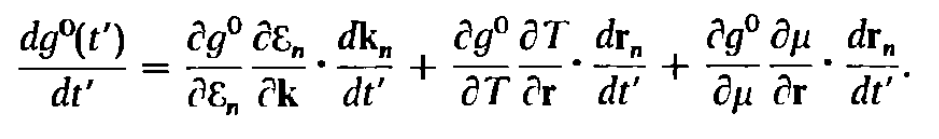
- From it we should see that, $g(t)$ depends on the $t'$ through two variables $r(t')$ and $k(t')$. For case-2 we have assumed that all the spatially dependent variables does not change, i.e $∇ T=$const., $\nabla \mu=$ const., $\nabla E=0$; it means the system is isotropic. No matter what is the value of $r(t')$ at which time $t'$, all the above mentioned values will be same.
- Hence, the $g(t)$ can depend on the $t'$ only through $k(t')$. The values relating to $k(t')$ are $v(k)$.
- Similarly the probability $P(t,t')$ contains the realxation time $\tau(t')$, hence, through $P(t,t')$ also the $g(t)$ depends on $t'$.
- If the magnetic field externally depends on the time, $E(t)$, then also the $g(t)$ will depend on the time $t'$ through it.
Case 3:
- In this case we assume that relaxation time depends only on the energy $\varepsilon(k)$, i.e. $\tau(\varepsilon(k)) \implies \tau(k)$. In the magnetic field the energy is always constant. In means the energy will take the value of only those $k$ for which $ε(k)$=const. In that case we can assume that the $\tau(\varepsilon(k)) \implies \tau(k)$.
- Besides as the equation for $g(t)$ contains the term $\partial f/\partial \varepsilon$ which for metals are non zero only around a very small $\delta k$ around the Fermi wave vector $k_{F}$. Hence we can assume that $\tau(\delta k) =$ const.
- The resulting distribution function is:

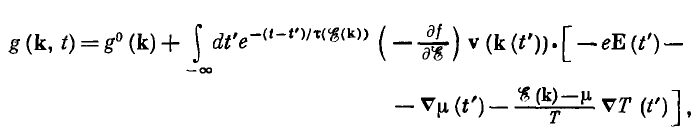
4. Application of distribution function

Five different examples can be presented showing the application of the general distribution function $g(k,t)$:
1. Conductivity tensor ($\sigma_{ij}$) due to static electric field (DC electrical conductivity)
2. Conductivity tensor ($\sigma_{ij}$) due to highly oscillating electric field (AC electrical conductivity)
3. Conductivity tensor under constant magnetic field (DC electrical conductivity under magnetic field)
4. Electrical conductivity due to temperature gradients (Seeback effect)
5. Thermal conductivity due to voltage gradient (Pelte effect)
The procedure for finding conductivity in any of the above case is following:
1. First observation is electrical current can be written through conductivity \[j=\sigma E.\]
2. In another formulation the electrical conductivity is the summation of the momentum of the electron $v(k)$ over all the occupied bands, which reads $j=\int\limits_{k, \text{occupied}} dk v(k)$. This equation is valid when the occupied states are independent of other time dependent parameters (electric field, magnetic field, temperature, chemical potential). However, in more general case the occupied states $k$ changes dynamically; it is taken care through the distribution function $g(k,t)$. Hence, the general equation for the current is \[j=\int\limits dk v(k) g(k,t).\] All the information of the occupied states are encoded inside the distribution function.
3. As $g(k,t)$ contains the electric field term $E(t)$, hence, we compare the conductivity equations in points (1) and (2) to find the expression for conductivity $\sigma_{ij}$.

4.1. DC electrical conductivity

In this case electric field is constant hence $E(t')$=const. Temperature — hence, chemical potential — along the space remains constant ($\nabla T=\nabla \mu =0$). Temperature is constant due to assumption. If temperature would not have been constant, then we will also have the Seeback effect.
Dependence of $k(t')$ on time can be neglected due to zero magnetic field. (Don't understand this point)
The conductivity takes the form:

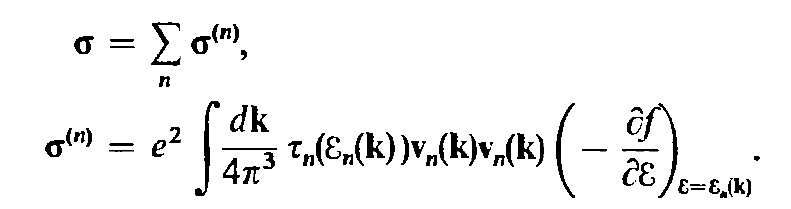
4.2. AC electrical conductivity

All the conditions as in DC case remains same expect for the extra $e^{\imath \omega t}$ term.
The conductivity is:

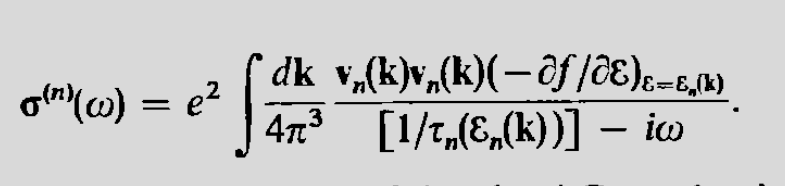
4.3. Seeback effect

To find the thermal conductivity we follow little bit other path. The thermal current $j^{q}$ is equal to the temperature multiplied by the entropy current \[j^{q}=Tj^{s}.\]
Change in entropy ($dS$) at constant temperature (T) is related to the change internal energy $dU$ and change in chemical potential ($\mu$) multiplied by the change in number of electrons ($dN$): \[dS = \frac{1}{T} \left( dU - \mu dN \right)\].
In terms of current above equations can be written as: \[Tj^{s} = j^{\varepsilon} - \mu j^{n}.\]
The energy and particle currents can be written as:
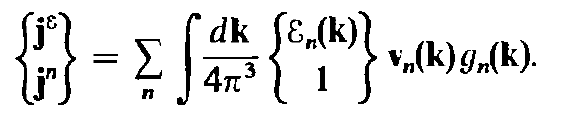
As $j^{q}=Tj^{s}$ and using the above equations for $j^{q}$ and $j^{n}$ we find the equation for the thermal current $j^{q}$ in terms of the distribution function $g(k,t)$.
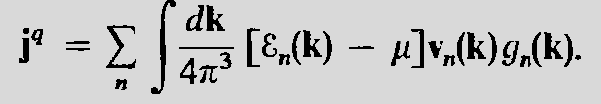
The $g(k,t)$ allows us to include the parameters $E(t'),\mu(t'),T(t')$ in the equations.
Little bit detour to represent the current in more general form.
- The above procedure gives a more general distribution function which considers both the thermal and electrical currents:
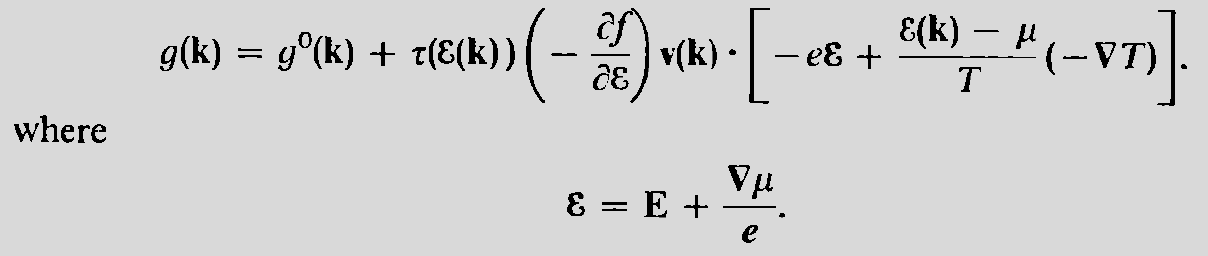
- We can represent both the current in terms of matrices
  \begin{equation} \begin{bmatrix} j \\ j^{q} \end{bmatrix} = \begin{bmatrix} L_{11} & L_{12}\\ L_{21} & L_{22} \end{bmatrix} \times \begin{bmatrix} \varepsilon\\ - \nabla T \end{bmatrix} \end{equation}
- where we define
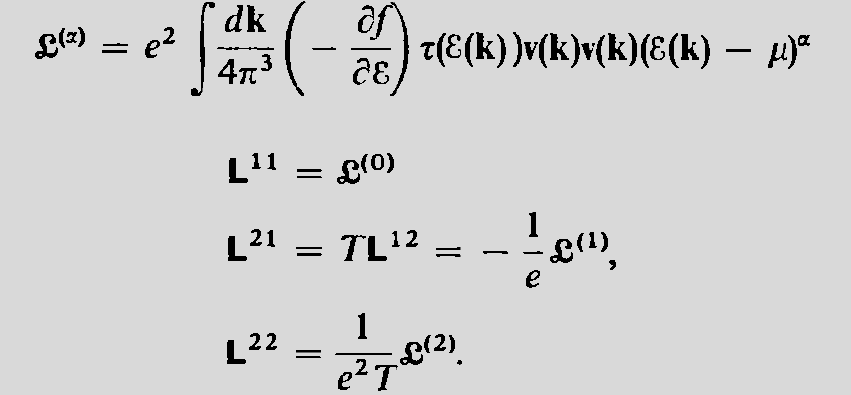
  - In case of metal only the states lying near the fermi surface contribute to the electrical properties, hence for $\alpha=1,2$ one use the Sommerfield expansion to get the thermoelectric equations for the metals:
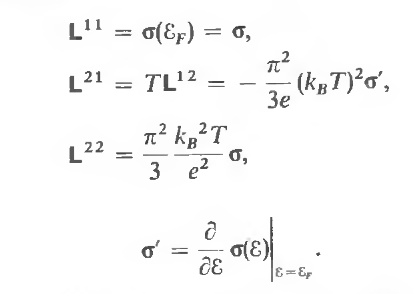
  - The thermal current is found from the condition that electric current is zero ($j=0$), from there we find the relation between $L^{11}$ and $L^{12}$. Using above equations for relations between $L^{11},L^{12},L^{21},L^{22}$ we will get the thermal current $j^{q}$: \[j^{q}=K \left( - \nabla T \right).\]
  - The Seeback effect is defined as the Voltage in between the two parts of the metal rod when a temperature gradient is present in them.
  - Some observations in measuring Seeback voltages:
    - The Seeback voltage can be measured correctly in bimetalic constructions with one of the metal as superconducting.
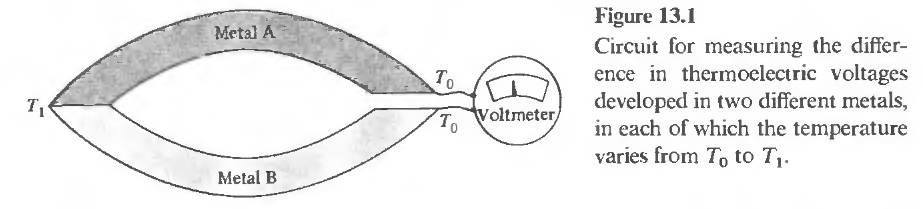
    - The reason being if the voltmeter is connected to the two end of the same metals with different temperature, then in the circuitry of the voltmeter will also develop voltage which will add to the actual voltage of the metal bar. Hence in the bimetal construction the voltmeter is connected to the two metals with same temperature. One of the metal is superconducting, because across superconductor no temperature gradient develops, and we measure the thermo electric voltage of the single material.
    - The voltmeter always measure not the electric potential but the electrochemical potential. Because apart from the current due to voltage across the metal there is also the current due to chemical potential difference. The chemical potential differ because at same temperature differnt metals have different chemical potentials. Hence voltmeter measures not $E$ but $\varepsilon = E + \nabla \mu$.
  - The thermo electric power $Q$ is defined as $\varepsilon = Q \nabla T$. One can from the first equation find that $Q = L^{12}/L^{11}$.
  - Important to understand the difference between thermal conductivity $K$ and thermo power $Q$. $K$ was found the relation between $J^{q} = K (-\nabla T)$, but $Q$ is found by relation between $\varepsilon = Q (\nabla T)$.

4.4. Peltier effect

It states that the isothermal electric current will be accompanied by the thermal current. Meaning if a current flows in the rod with constant temperature across the rod, then the current will be accompanied by the thermal current.
To measure it one can use the bimetallic construction:
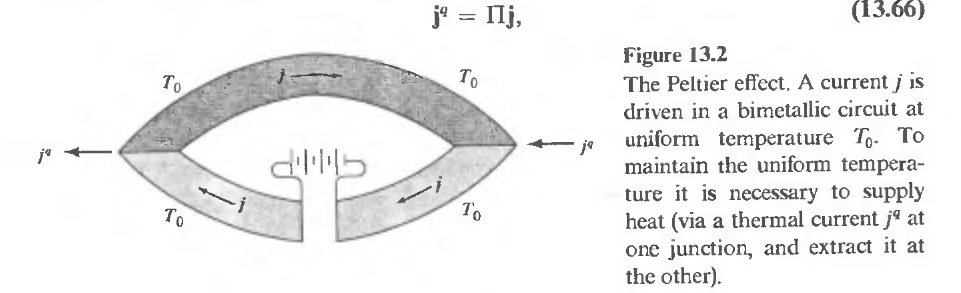
The peltier coefficient is defined as: \[j^{q}=\Pi j.\]
It can be found from the previous two equations by putting $\nabla T=0$.
It is related to the thermopower as: \[\Pi = T Q.\]
Notes: Related to the thermal effects we have three quantities:
1. Thermal conductivity $K$; $j^{q}=K(-\nabla T)$ (derived by putting current $j=0$)
2. Thermal Power $Q$; $\varepsilon = q \nabla T$ (derived by putting current $j=0$)
3. Peltier coefficient $\Pi$; $j^{q}= \Pi j$ (derived by putting $\nabla T=0$)

5. Distribution function when $H \neq 0$

When magnetic field is not equal to zero all the above analysis is not valid, because in $g(k,t)$ we can not replace $k(t')=k$, as now $k(t')$ depends on the relaxation times upto time $t$.

Semi-Classical Theory of Conduction in Metals

Table of Contents

1. Relaxation time approximation

2. Non-equilibrium distribution function

3. Simplification of the distribution functions

4. Application of distribution function

4.1. DC electrical conductivity

4.2. AC electrical conductivity

4.3. Seeback effect

4.4. Peltier effect

5. Distribution function when \(H \neq 0\)