Semi-Classical Treatment

Table of Contents

1. Difference of the semi-classical electrons from others

  • The Drude theory treat the electrons as complete classical particle. Sommerfeld treated the electrons as the quantum mechanical particles (waves) but did not considered the background potential due to ions. Bloch treated the electrons as quantum mechanical particles (waves), however considered the background periodic potential due to ions. Both Sommerfeld's and Bloch's treatment are quantum mechanical in nature. Between classical and quantum mechanical treatment there exists the quasi-classical treatment of the electrons. In this case the electrons are treated as wave packets, i.e. they are summation of the momentum \(\Delta k'\) around given \(k\).
  • In the quasi-classical case the electrons wave functions are couple of lattice unit wide. To treat the problem under quasi-classically under externally applied field, the applied field should at least tens of lattice unit wide.

2. The main assumptions of the semi-classical treatment

  • It is assumed that the energy dispersion of the particular band \(\varepsilon_{n}(k)\) is known before hand. The semiclassical treatment do not give the energy dispersion, but acts on the already available energy dispersion to find dynamical quantities, \(\dot{k}\) and \(\dot{r}\) of the system.
  • The band number \(n\), position \(r\) and the wave number \(k\) are the quantum numbers of the system.
  • It is assumed that the band number \(n\) remains constant. One way of explaining this is due to fact that in semi-classical theory we are considering only low energy electrons. The low energy electrons comes from the fact that the electronic wave packet is spread across tens of atomic site. It is found from the fact that we assumed that uncertainty in the wave packet \(\Delta k < 2\pi/a\) is inside the Brillouin zone. Hence from the Heisenberg's uncertainty principle \(\Delta k \Delta x > \hbar\) we find \[\Delta x > \hbar/\Delta k \implies \Delta x > \hbar a /2 \pi\]. The highest energy electrons have the wave vectors \(k=2\pi/a\), physically it means the waves change the phase by \(2\pi\) in one atomic units. It is clearly higher than the above mentioned semi-classical long wavelength limits.

  • The dynamic equations are:

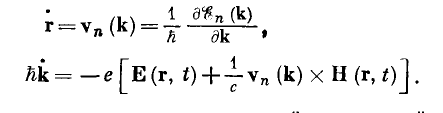
    dynamic-eqn.png

    The first equation gives the momentum \(v_{n}(k)\), and second equation gives the external force applied on the electron. It follows from the fact that change in momentum is equal to the externally applied field.

3. Typical characteristic of semi-classical model

  • Although the material can have large number of bands, however, we consider only that (or those) bands through which the Fermi energy \(E_{f}\) goes through. Specifically only those states, which are in the vicinity of \(|k_{B}T|\) of \(E_{f}\). It should be noted that \(k_{B}T\) is normally not greater than energy gaps. Usual energy gaps have energy of $∼ 10-1$eV. The value of $kB ≈ 8.62 × 10-5$eV/K. Even at room temperature $T=330$K the energy gap \(E_{f} \gg k_{B}T\) by 100 times.
  • According to the definition of the momentum, it is related to the applied force on the particle: the rate of change of momentum of the particle is equal to the force applied on the particle. In above equation \(\hbar \dot{k}\) represents only change due to the externally applied field, hence, it is quasi momentum.

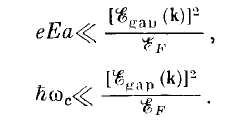
  • The applied field should satisfy the following two conditions, so that semi-classical approximation will be applicable to the problem: field-limits.png

    The first term is related to the electric field; physically it means the energy accumulated by the electron in between two collisions (minimum free path between collision is distance between atoms \(a\)) should be much smaller than the energy gap. The second term is related to the magnetic field. The cyclotron frequency \(\omega_{c}=e H/mc\) is related to the energy induced by the magnetic field into the electrons; more higher the value of \(\omega_{c}\) the faster the electrons circles, the higher the energy will be. This is very back of the hand calculation.

  • Another condition is that the frequency of the applied field should be less than the energy gap. As if the energy will be greater than the energy gap, then electrons at the fermi levels may jump to other band. The energy of the applied field is measured through its frequency, it is defined as \(\hbar\omega< \varsigma_{gap}\).
  • The last condition is that the wave length of the applied field should be greater that couple of atomic distances. On the other hand the assumption that we are working only with low energy electrons is violated, as energy at the BZ starts to pitch in different process.

4. Important physical effect due to semi-classical treatment

4.1. A completely filled band can not conduct electric or thermal current

  • It can be proved from the point of view of the density of states in \(r-k\) phase space. Under external field the coordinates (\(r\)) and momentum (\(k\)) transform according to the above dynamic equation. As both of them are linear function of the time \(t\):

    \begin{equation*} \begin{aligned} &r = v_{n}(k) t = \frac{1}{\hbar} \frac{\partial \varepsilon_{n}(k)}{\partial k} \times t\\ &k = -\frac{1}{\hbar} e E \times t \end{aligned} \end{equation*}

    All the states \((r,k)\) increases accordingly a fixed trajectory. Hence the initial density of states does not changes in the phase space in between two collisions.

  • During collisions one can expect that the momentum \(k\) can be changed after collision. However, in following two cases we expect no change is density of staes:

    1. When the band is fully occupied and Fermi level lies in the band gap.
    2. When the Fermi level is within the band but the system is in thermodynamical equilibrium.

    In the first case the electrons don't have available empty states to jump to within band; moreover, interband transition is prohibited. In the second case the thermodynamic equilibrium does not allow for electron to stay long in any other states outside equilibrium. Hence, even if electron is excited to another state outside thermodynamic equilibrium it returns to the equilibrium states instantly.

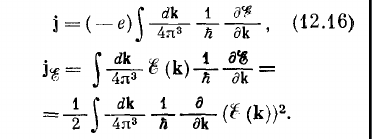
  • Another way to prove this is just taking the integral of the current operator over whole BZ. As the current operator involves the velocity of the electrons (\(v(k)=\partial \varepsilon/\partial k\)) which is a periodic function over the Brillouin zone, hence the integration of whole BZ will give zero value. The current operators are: current-opr.png
  • On a side note one can say that, the system where all the zones are filled, it has even number of electrons. This is true as considering the spins to every energy level corresponds two states.
  • On the other hand one can not say that, if the system has even number of electrons, then it can not have completely full zone. This is true as one fills the states from the bottom situations arise when the next band has lower energy then the present band. In that case electron and hole pockets arises in the system. This can be understood for the square lattice and free electron picture: square-lat.png

4.2. Under external electric field acceleration of electrons are opposite to the applied electric field

  • The change in electric momentum \(k\) due to electric field can be found from the semi-classical dynamic equations:

    \[k(t)=k(0)-\left(eEt/\hbar \right).\]

  • Two cases can be analysed:
    • Fully filled zone
    • Partially filled zone

  • In case of fully filled zone the applied electric field does not create any current. As all the electrons are shifted by same amount. Because the states of electrons are same shifted by the BZ vector, hence, at any point of time, the total left travelling electrons will be same as the right traveling electrons. Hence, the total current will be zero always.

    Elec-field-filled-bz.jpg

  • In case of the partially filled zone, for monotonical increase in \(k(t)\) one expects the AC current. At equilibrium both the negative and positive \(k\) are filled upto same amount, hence, the total left travelling electrons are same as the total right travelling electrons. However if the electric field is applied the equilibrium will be broken. Depending on the direction of the applied electric field the left travelling and right travelling electrons will not cancel each other. Which will result in the electric current.

    current-dc.jpg

  • However, if the \(k(t)\) would have increased monotonically unbounded, we would have expected the alternating current (due to the periodic nature of the energy dispersion); this does not happen. The reason is the collision. In other words for ac current to appear all the states should be transfered by the reciprocal lattice vector. current-ac.jpg
  • Another interesting fact about the periodic nature of the velocity, is it is zero at the boundaries of the BZ. In other words the closer the system is at the boundaries the higher the probability of the states being Bragg reflected. Bragg reflection is the condition when the one state can be transfered to its negative image by a reciprocal lattice vector. If \(\mathbf{k}\) is some momentum and \(\mathbf{G}\) is the reciprocal lattice vector. Then the momentum \(\mathbf{k}' \approx \mathbf{k}+\mathbf{G}\). This condition is satisfied at the boundaries of the BZ. bragg-reflection.jpg

4.3. The theory of Holes

  • The physical reason being, the velocity of electron \(v(k)=\partial \varepsilon/\partial k\) changes with the time as \(k(t)=k(0) + eEt\). If the \(k\) lies at the BZ boundary then with time the \(v(k)\) might change from zero to negative. It means electron wave packet travels in the opposite direction. The behaviour is same as if a positively charged particle is travelling, this is known as hole. As it is possible only at the boundary of BZ hence, the effect is usually observed at the maximum of the energy band.
  • The reduced mass comes from the definition of the holes. At the isotropic band maximum the energy dispersion can be thought of as quadratic function which can be approximated as: \(\varepsilon(k) \approx \varepsilon(k_{0}) - A(k-k_{0})\). It is found from the Taylor expansion of the energy dispersion. From here one can represent \(A=\hbar^{2}/2m^{\ast}\), however, the actural value of \(A\) is \(A=\frac{\partial^{2} \varepsilon(k)}{\partial k^{2}}\). At the band minimum it is positive hence the electrons are present at band minimum and at band maximum it is negative, hence holes are present at band maximum.
  • The idea of hole is given in following figure. hole.jpg

4.4. Motion of semi-classical electrons under magnetic field

  • Under magnetic field electrons always travel on the isoenergy surface, perpendicular to the magnetic field. It can be understood from the equation of motion of electrons: 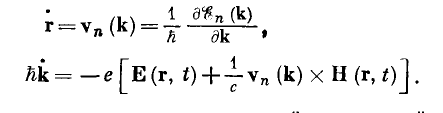dynamic-eqn.png The \(v(k)\) is the gradient of the energy dispersion. Physically it means it is aligned along the direction of the highest change in energy in the momentum space. The \(\hbar \dot{k}\) is aligned along the direction which is perpendicular to both \(v(k)\) and magnetic field \(H\). Assuming the direction of the magnetic field to be along $z$-axis, then \(\hbar \dot{k}\) will be on the \(x-y\) plane. Besides the \(\hbar \dot{k}\) should also be perpendicular to the \(\partial E / \partial k\); it means, as \(\partial E / \partial k\) is along the direction of the highest change in energy on the \(k_{x}-k_{y}\) plane, perpendicular to it will be along the direction of the zero-energy changes. It means the direction of the \(\hbar \dot{k}\) will be along the isoenergy surface.
  • The trajectory of electrons in the real space can be found by rotating the trajectory in the momentum space by \(\pi/2\) in the anti-clockwise direction. It can be found from the equation involving \(\hbar \dot{k}\), and writing \(\dot{k}=dk/dt\) and \(v=dr/dt\).
  • Trajectory of electron also gives the time period of electron to traverse the closed Fermi surface, corresponding to the single energy. The time period is related to the total area closed inside the trajectory of the electrons. It is a function of energy and the \(k_{z}\) cut of the fermi surface: $$T(ε, kz) = \frac{ℏ2c}{e H} \frac{∂ A(ε, kz)}{∂ ε}. It shows that the time period is inversely proportional to the applied field \(H\), and directly proportional to the trajectory in the momentum space.
  • One also introduces the cyclotron mass to get the time period in a more tractable form: \[T= \frac{2 \pi}{\omega_{c}}= \frac{2 \pi m c}{e H}.\] Comparing this time period \(T\) with the time period \(T(\varepsilon, k_{z})\) we will get the effective cyclotron mass: \[m^{\ast}(\mathcal{E},k_{z})= \frac{\hbar^{2}}{2\pi} \frac{\partial A(\mathcal{E},k_{z})}{\partial \mathcal{E}}.\]

4.5. Motion of electron in magnetic field and Electric field consists of just translation of the fermi surface

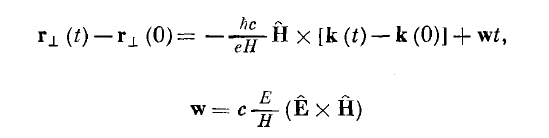
  • If apart from magnetic field, electric field is also applied to the system then the shape of the trajectory of the electron will remain same as in the magnetic field. The only difference is that, now the trajectory will start to slide on the plane perpendicular to the magnetic field, and along the direction perpendicular to both magnetic and electric field. motion-in-E-H.png

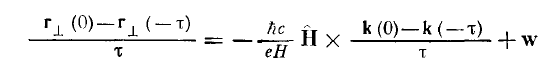
  • Magneto resistance under strong magnetic field is divided into two cases: (i) when all the electron and hole orbits are closed, (ii) when part of the electron or hole orbits are opened. In both these cases the following equation is applicable for the velocity of the electron under an external field: velo-mag-resis.png

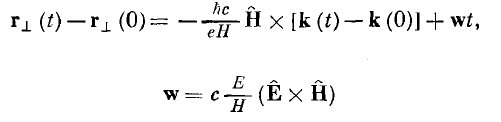
    It is found from the velocity equation under electric and magnetic field: velo-under-E-H.png

  • The effect of the \(w\) is to just translate the Fermi surface by the amount \(|w|\) along the opposite direction of the \(w\). FS-translation.jpg

4.6. Magneto resistance

  • Now we discuss the first case. We see that both the magnetic and electric field part of the velocity is inversely proportional to the applied magnetic field. However the magnetic field part also depends on the change in the momentum \(k(t)\). As we have assumed that the orbit of the electrons are closed and electrons can travel numerous times along the orbit before collision the value of \(k(0)-k(\tau) \approx 0\). Hence the main contribution to the current \(j=-nev\) comers from the electric field part \(w\). Physically it means the closed orbit of the electrons drifts along the direction perpendicular to the applied electric and magnetic field with velocity \(w\). In the presence of both the electron and holes in the band of the system, i.e. partially filled electronic bands. Then the total current \(j=-(n_{eff} \: ec/H) (E \times H)\) will be the difference in the density of the electron and holes (\(n_{eff}\)). Magnetoresistance becomes constant in the closed orbit case at high magnetic field, or if a band is half-filled. It increases for doped materials.

Author: Каушаль Кешарпу

Created: 2025-06-29 Вс 18:33

Validate